Hình thang vuông là hình như thế nào, công thức tính diện tích hình thang vuông và chu vi hình thang vuông ra sao? Tất cả sẽ được Hyundai Smart Phone giải dáp hình thang vuông là gì, tính chất và công thức tính chu vi, diện tích hình thang vuông kèm theo bài tập có lời giải chi tiết tại đây
Hình thang vuông là gì?
Hình thang vuông là hình thang có một góc vuông. Nói cách khác hình thang vuông là một trong những trường hợp đặc biệt của hình thang.
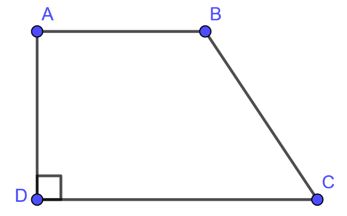
Tứ giác ABCD là hình thang vuông (đáy AB, CD) ⟺ ∠A = ∠D= 90∘ hoặc ∠B = ∠C= 90∘
Dấu hiệu nhận biết hình thang vuông
Hình thang có một góc vuông là hình thang vuông
Tình chất hình thang vuông
Hình thang vuông có hai cạnh đáy song song và vuông góc với hai đáy, tạo nên góc 90 độ.
Công thức tính chu vi hình thang vuông
Chu vi hình thang vuông được tính bằng tổng các cạnh bên và cạnh đáy
P = a + b + c + d.
Trong đó:
- P: Chu vi hình thang.
- a,b: Lần lượt là độ dài 2 cạnh đáy.
- c,d: Lần lượt là đội dài 2 cạnh bên.
Công thức tính diện tích hình thang vuông
Diện tích hình thang vuông bằng tổng độ dài hai cạnh đáy nhân với chiều cao, sau đó tất cả chi cho 2. Nói cách khác, diện tích hình thang vuông bằng ½ tích chiều cao hạ từ cạnh đáy a xuống b nhân với tổng độ dài hai cạnh đáy.
S = ½h.(a+b)
Trong đó:
- S: diện tích của hình thang vuông.
- a, b: độ dài của 2 cạnh đáy.
- h: chiều cao hình thang (độ dài cạnh vuông góc với 2 đáy).
Tham khảo thêm: Công thức tính diện tích tam giác vuông, đều, cần kèm VD có lời giải
Các dạng bài tập về hình thang vuông có lời giải
Dạng 1. Tính số đo góc
Phương pháp giải: Sử dụng tính chất hai đường thẳng song song và tổng bốn góc trong một tứ giác kết hợp với kiến thức đã học về hình thang vuông.
Ví dụ 1: Hình thang vuông ABCD có Aˆ = Dˆ = 900; AB = AD = 3cm;CD = 6cm. Tính số đo góc B và C của hình thang?
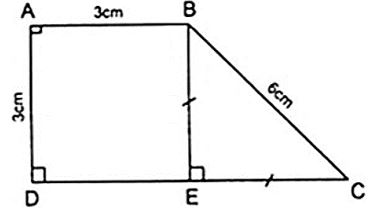
Lời giải
Kẻ BE ⊥ CD thì AD//BE (do cùng vuông góc với CD) nên hình thang ABED có hai cạnh bên song song.
Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang ABED và giả thiết ta được BE = DA = 3cm; DE = AB = 3cm,
Do đó: EC = DC – DE = 6 – 3 = 3cm.
Suy ra ΔBEC vuông cân tại E nên Cˆ = 450
Do góc ABCˆ và Cˆ là hai góc trong cùng phía của AB//CD nên chúng bù nhau hay
ABCˆ + Cˆ = 1800 suy ra ABCˆ = 1800 – 450 = 1350
Vậy hình thang có Bˆ = 1350 và Cˆ = 450
Ví dụ 2: Cho hình thang vuông ABCD có Aˆ = Dˆ = 900, AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang
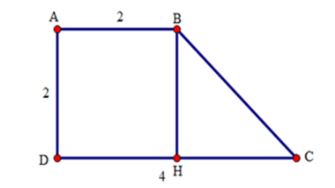
Lời giải
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD//BH (cùng vuông góc với CD)
nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân tại đỉnh H.
Lại có BHCˆ = 900 do BH ⊥ CD nên tam giác BHC vuông cân tại H.
Do đó BCHˆ = 450
Xét hình thang ABCD có:
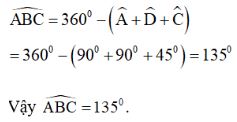
Dạng 2: Chứng minh hình thang vuông
Phương pháp giải: Sử dụng định nghĩa hình thang vuông
Ví dụ 1: Cho tam giác ABC vuông cân tại A. Vẽ về phía ngoài tam giác ACD vuông cân tại D. Tứ giác ABCD là hình gì? Vì sao?
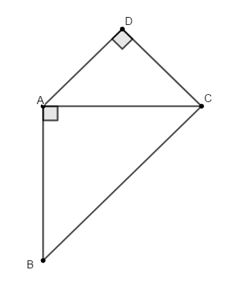
Lời giải
Vì tam giác ABC là tam giác vuông cân tại A
⇒ ABCˆ = ACBˆ = 450
Vì tam giác ADC là tam giác vuông cân tại D
⇒ DACˆ = DCAˆ = 450
Do đó: DACˆ = ACBˆ = 450
Mà DACˆ và ACBˆ là hai góc so le trong
Do đó: AD // BC
Xét tứ giác ABCD ta có:
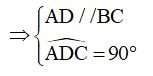
Suy ra ABCD là hình thang vuông.
Dạng 3. Sử dụng các tính chất của hình thang vuông để chứng minh bài toán
Phương pháp giải: Áp dụng các tính chất về cạnh và góc của hình thang vuông đã học để giải quyết bài toán
Ví dụ 1: Cho hình thang vuông ABCD có Aˆ = Dˆ = 900, AB = AD, DC = 2AB và BE vuông góc với CD tại E.
a) Chứng minh: ΔABD = ΔEDB
b) Chứng minh: ΔBEC vuông cân tại E.
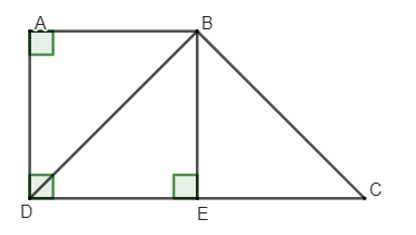
Lời giải
a) Do ABCD là hình thang nên AB // CD
ABDˆ = BDCˆ (hai góc so le trong)
Vì BE ⊥ DC ⇒ BED = 900
Xét ΔABD và tam giác ΔEDB ta có:
BD chung
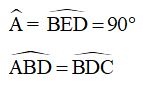
Do đó: ΔABD = ΔEDB (cạnh huyền – góc nhọn)
b) Từ hai tam giác bằng nhau ở câu a ta có:
AB = ED; AD = EB (các cặp cạnh tương ứng)
Mà AB = ½CD ⇒ ED = ½CD
Suy ra E là trung điểm của CD
=> ED = AB = EC
Mà AB = AD (giả thuyết)
Nên ED = AB = EC = AD = EB
Xét tam giác BEC có
EB = EC
BECˆ = 900
Vậy ΔBEC là tam giác vuông cân tại E
Dạng 4: Tính chu vi, diện tích hình thang vuông
Phương pháp: Sử dụng công thức tính chu vi, diện tích hình thang vuông
Ví dụ 1: Hình thang ABCD (AB//CD) có AB = 4cm, CD = 8cm, và AD = 5cm. Tính diện tích hình thang ABCD.
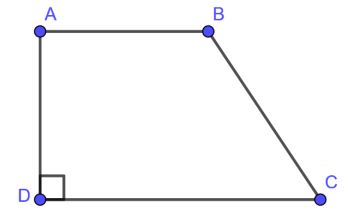
Lời giải
Hình thang ABCD có AB//CD nên hai đáy là AB, CD.
AD ⊥ DC
suy ra AD là chiều cao của hình thang.
Vậy diện tích của hình thang ABCD là S = ½ h.(a + b) = ½ .5.( 4 + 8) = 30 cm2
Ví dụ 2: Cho hình thang vuông có khoảng cách 2 đáy là 16cm, đáy nhỏ bằng ¾ đáy lớn. Tính độ dài 2 đáy khi biết được diện tích hình thang vuông là 112cm².
Giải:
Khoảng cách 2 đáy trong hình thang vuông chính là chiều cao hình thang nên:
Tổng độ dài hai đáy là (112 x 2) : 16 = 14cm
Ta gọi độ dài đáy bé là a, độ dài đáy lớn là b, ta có:
a + b = 14 và a = ¾ b
Nên a = (14 x 4): 7 = 8cm
Do đó, đáy bé = 34⁄7 cm, đáy lớn 64⁄7 cm
Ví dụ 3: Cho hình thang ABCD có hai đáy là AB và CD. Biết AB = 15cm, CD = 20cm, chiều cao hình thang là 14cm. Hai đường chéo AC và BD cắt nhau ở E. Tính diện tích hình thang ABCD
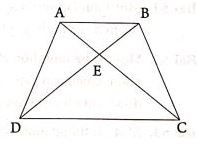
Lời giải:
Gọi S là diện tích hình ABCD thì
S = ½h.(a+b) = ½.14.(15+20 ) = 245 cm2
Ví dụ 4: Cho hình thang vuông ABCD có AD = 6 cm ; DC = 12 cm ; AB = 2⁄3DC
a) Tính diện tích hình thang ABCD
b) Khi kéo dài cạnh bên AD và CB thì 2 cạnh bên này cắt nhau tại M. Tính độ dài cạnh AM
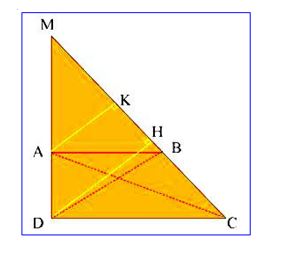
Lời giải
a) Độ dài cạnh AB là:
AB = 2⁄3 DC = 12 . (2/3) = 8 cm
Diện tích ABCD : (8 + 12) / 2 . 6 = 60 cm
b) Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau và bằng 6 cm, đáy AB = 2⁄3 CD
⇒SABC = 2⁄3 SDBC
Xét tiếp hai tam giác ABC và DBC đáy BC vì SABC = 2⁄3 SDBC ⇒ chiều cao AK = 2⁄3 DH
Xét tiếp tam giác AMC và tam giác DMC chung đáy MC mà chiều cao AK = 2⁄3 DH ⇒ SAMC = 2⁄3SDMC. SDMC lớn hơn SAMC (12. 6) / 2 = 36 cm2
SAMC = 36 / (3-2). 2 = 72 cm2
Xét tam giác AMC đáy AM, chiều cao CD ⇒ AM = 72 . 2 / 12 = 12 cm
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn nắm được hình thang vuông là gì, tính chất, dấu hiệu nhận biết và công thức tính diện tích hình thang vuông, chu vi hình thang vuông để áp dụng vào làm bài tập rồi nhé




