Tìm m để hàm số đồng biến, nghịch biến trên khoảng kèm VD

Trong các đề thì hay bài kiểm tra có rất nhiều bài tập tìm m để hàm số đồng biến trên khoảng, hoặc m để hàm số nghịch biến trên khoảng. Do đó, Hyundai Smart Phone sẽ hướng dẫn các bạn tìm tìm m để hàm số đồng biến, nghịch biến trên khoảng kèm theo bài tập có lời giải chi tiết trong bài viết dưới đây

Hàm số đồng biến, nghịch biến khi nào?

1. Hàm số đơn điệu là gì?

Giả sử hàm số y = f (x) xác định trên K, với K là một khoảng, một đoạn hoặc một nửa khoảng.

• Hàm số y = f (x) được gọi là đồng biến trên K nếu: ∀x₁, x₂ ∈ K, x₁ < x₂ : f (x₁) < f (x₂)
• Hàm số y = f (x) được gọi là nghịch biến trên K nếu: ∀x₁, x₂ ∈ K, x₁ < x₂ : f (x₁) > f (x₂)
• Hàm số đồng biến hoặc nghịch biến được gọi chung là hàm số đơn điệu trên K.

2. Điều kiện cần và đủ để hàm số đơn điệu

a. Điều kiện cần để hàm số đơn điệu:

Giả sử hàm số y = f (x) có đạo hàm trên K. Khi đó:

• Nếu hàm số y = f (x) đồng biến trên K thì f ‘(x) ≥ 0, ∀x ∈ K.
• Nếu hàm số y = f (x) nghịch biến trên K thì f ‘(x) ≤ 0, ∀x ∈ K.

b. Điều kiện đủ để hàm số đơn điệu:

Giả sử hàm số y = f (x) có đạo hàm trên khoảng K. Khi đó:

• Nếu f ‘(x) > 0, ∀x ∈ K thì hàm số f (x) đồng biến trên khoảng K.
• Nếu f ‘(x) < 0, ∀x ∈ K thì hàm số f (x) nghịch biến trên khoảng K.
• Nếu f ‘(x) = 0, ∀x ∈ K thì hàm số f (x) không đổi trên khoảng K.

Định lí: Giả sử hàm số y = f (x) có đạo hàm trên khoảng K.

Hàm số y = f (x) đồng biến trên K thì f ‘(x) ≥ 0, ∀x ∈ K và f ‘(x) = 0 chỉ xảy ra tại hữu hạn điểm của t.

Hàm số y = f (x) nghịch biến trên K thì f ‘(x) ≤ 0, ∀x ∈ K và f ‘(x) = 0 chỉ xảy ra tại hữu hạn điểm của t.

Cách tìm m để hàm số đồng biến, nghịch biến trên khoảng

1. Tìm m để hàm số đồng biến, nghịch biến trên từng khoảng xác định

Chương trình phổ thông ta thường gặp dạng bài này đối với hàm số đa thức bậc 1 trên bậc 1, ta sẽ áp dụng chú ý sau:

2. Tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước.

Cách 1:

Cách 2: Cô lập tham số m

Bước 1: Tìm y’

Bước 2: Cô lập m ta sẽ thu được phương trình ví dụ m ≥ f(x)

Bước 3: Xét dấu với hàm f(x) theo bảng quy tắc sau:

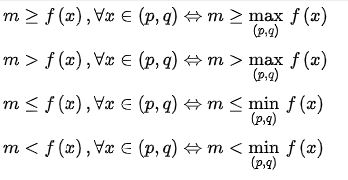
Tham khảo thêm: Cách tính lim thủ công, máy tính đơn giản kèm theo VD từ A – Z

Bài tập tìm m để hàm số đồng biến, nghịch biến trên khoảng

1. Dạng 1: Tùy theo tham số m khảo sát tính đơn điệu của hàm số

Trong chương trình, đây là dạng toán thường gặp đối với hàm số đa thức bậc 3. Nếu là hàm đa thức bậc 3 thì chúng ta có thể áp dụng kiến thức sau:

Ví dụ 1: Tìm m để hàm số y = x³/3 – mx²+(1 – 2m)x- 1 đồng biến trên (1; +∞)

Lời giải

TXĐ: D = R

Ta có y’ = x² – 2mx + 1 – 2m

Hàm số đã cho đồng biến trên (1; +∞)⇔ ∀ x ∈(1; +∞),y’ ≥ 0

⇔ ∀ x ∈ (1; +∞), x² -2mx + 1 – 2m ≥ 0 ⇔ ∀ x ∈(1; +∞), x² + 1 ≥ 2m(x + 1)

⇔ ∀ x ∈(1; +∞),2m ≤ (x² + 1)/(x + 1) (do x + 1 > 0 khi x > 1)

Xét hàm số f(x) = (x²+ 1)/(x + 1), x ∈ (1; +∞)

f'(x) = (x² + 2x – 1)/(x + 1)2 >0 với mọi x ⇔ (1;+∞)

Ta có bảng biến thiên:

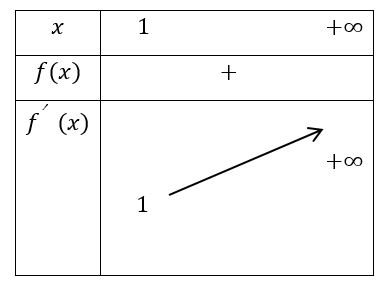
Dựa vào bảng biến thiên để 2m ≤ f(x),∀ x ∈(1; +∞) thì 2m ≤ 1 ⇔ m ≤ 1⁄2

Ví dụ 2: Cho hàm số y = x³ – 3mx² + 3(m² – 1)x – 2m + 3. Tìm m để hàm số nghịch biến trên khoảng (1; 2).

Lời giải:

Tập xác định: D = R

Đạo hàm y’ = 3x² – 6mx + 3(m²-1)

Hàm số nghịch biến trên khoảng (1; 2 )⇔ y’ ≤ 0 ∀ x ∈ (1; 2)

Ta có Δ’= 9m² – 9(m2-1)= 9 > 0 ∀m

Suy ra y’ luôn có hai nghiệm phân biệt x₁ = m – 1; x₂ = m + 1(x₁<x₂)

Do đó y’ ≤ 0 ∀ x ∈(1;2) ⇔ x₁ ≤ 1 < 2 < x₂

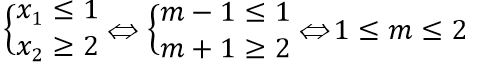
Vậy giá trị m cần tìm là 1 ≤ m ≤ 2

2. Dạng 2: Tìm m để hàm số đồng biến, nghịch biến trên R

Phương pháp giải: sử dụng định lý về điều kiện cần

• Nếu hàm số f đồng biến trên R thì f ‘(x) ≥ 0 với mọi x ∈ R
  Nếu hàm số f nghịch biến trên R thì f ‘(x) ≤ 0 với mọi x ∈ R

Ví dụ 1: Hàm số y = x³ + 3x² + mx + m đồng biến trên tập xác định khi giá trị của m là bao nhiêu?

Lời giải

Tập xác định D = R

Tính đạo hàm y’ = 3x² + 6x + m

Để hàm số đồng biến trên R ⇔ y’ ≥ 0 ⇔ 3x² + 6x + m ≥ 0 với mọi x ∈ R (*)

⇔ Δ’ ≤ 0 ⇔ 9 – 3m ≤ 0 ⇔ m ≥ 3

Ví dụ 2: Cho hàm số Tìm tất cả giá trị của m sao cho hàm số luôn nghịch biến.

Lời giải

Tập xác định: D = R

Tính đạo hàm: y’ = (1 – m)x² – 4(2 – m)x + 4 – 2m

TH1: Với m = 1 ta có:

y’ = -4x + 2 ≤ 0 ⇔ x ≥ 1⁄2

Vậy m = 1 không thỏa mãn điều kiện đề bài.

TH2: Với m ≠ 1 ta có:

Hàm số luôn nghịch biến

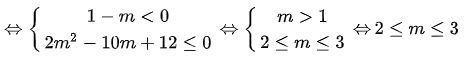
3. Dạng 3 : Tìm m để hàm số đơn điệu trên tập con của R

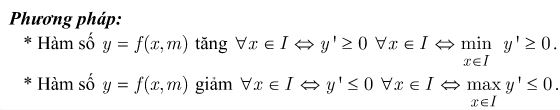
Ví dụ 1: Tìm tất cả các giá trị của tham số m để hàm số y = 1⁄3x³ + (m-1)x² + (2m – 3)x -2⁄3 đồng biến trên (1;+∞)

Lời giải

Hàm số đồng biến trên khoảng (1;+∞) ⇔ y’ ≥ 0; ∀ x ∈ (1;+∞)

Ta có y’ = x² + 2(m – 1)x + 2m – 3 = (x + 1)(x + 2m – 3) ≥ 0; ∀ x ∈ (1;+∞)

Do x > 1 nên (x + 1) > 0, nên (x + 2m – 3) ≥ 0 với mọi x > 1.

2m – 3 ≥ -x; ∀ x > 1 ⇔ 2m – 3 ≥ -1 ⇔ m ≥ 1.

Ví dụ 2: Tập hợp các giá trị m để hàm số y = mx³ – x² + 3x + m – 2 đồng biến trên (-3;0)

Lời giải

TXĐ: D = R

Ta có y’ = 3mx² – 2x + 3. Hàm số đồng biến trên khoảng (-3;0) khi và chỉ khi:

y’ ≥ 0, ∀ x ∈ (-3;0) (Dấu “=” xảy ra tại hữu hạn điểm trên (-3;0))

4. Dạng 4. Biện luận đơn điệu của hàm phân thức

Phương pháp giải được chia thành 2 loại như sau:

Loại 1. Tìm điều kiện của tham số để hàm y = ax + b/cx + d đơn điệu trên từng khoảng xác định.

Tính y’ = (ad – cb)/ (cx + d)²

• Hàm số đồng biến trên từng khoảng xác định của nó ⇔ y’ > 0 ⇔ ad –cb > 0
• Hàm số nghịch biến trên từng khoảng xác định của nó ⇔ y’ < 0 ⇔ ad –cb < 0

Ví dụ 1: Cho hàm số y= x+m−2/x−m

a) Tìm m để hàm số nghịch biến trên mỗi khoảng xác định.

b) Tìm m để hàm số nghịch biến trên khoảng (5;+∞).

Lời giải

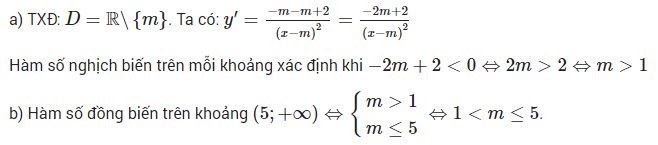
Ví dụ 2: Tìm tập hợp tất cả các tham số thực của m để hàm số y = x³ – (m + 1)x² + 3 x+ 1 đồng biến trên khoảng (-∞;+∞).

Lời giải:

+ Tập xác định D = R.

+ Ta có y’ = 3x² – 2(m + 1)x + 3.

+ Hàm số y = x³ – (m + 1) x² + 3x + 1 đồng biến trên khoảng (-∞; +∞)

⇔ y’ ≥ 0,∀x∈R

⇔ Δ’ ≤ 0 ⇔ (m + 1)² – 9 ≤ 0 ⇔ m² + 2m – 8 ≤ 0 ⇔ -4 ≤ m ≤2.

Vậy giá trị của tham số m cần tìm là -4 ≤ m ≤ 2

Sau khi đọc xong bài viết của chúng tôi có thể giúp bạn biết cách tìm m để hàm số đồng biến trên khoảng và tìm m để hàm số nghịch biến trên khoảng rồi nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi