Xin gửi đến các bạn Bảng Nguyên Hàm cơ bản, hàm nâng cao, hàm mở rộng, hàm hợp, hàm đặc biệt, hàm Logarit…Bên dưới đây là các công thức nguyên hàm đầy đủ nhất các bạn đón xem.
Định nghĩa và tính chất của nguyên hàm
1. Định nghĩa
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Kí hiệu: ∫ f(x)dx = F(x) + C.
Định lí 1:
1) Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.
2. Tính chất của nguyên hàm
• (∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
• Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
• ∫ kf(x)dx = k∫ f(x)dx với k là hằng số khác 0.
• ∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx.
3. Sự tồn tại của nguyên hàm
Định lí:
Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
Bảng nguyên hàm và công thức cơ bản
=> Mình xin chia sẻ đến mọi người bảng nguyên hàm và các công thức cơ bản nhất

Bảng nguyên hàm và công thức mở rộng
=> Bảng nguyên hàm và các công thức nguyên hàm dạng mở rộng
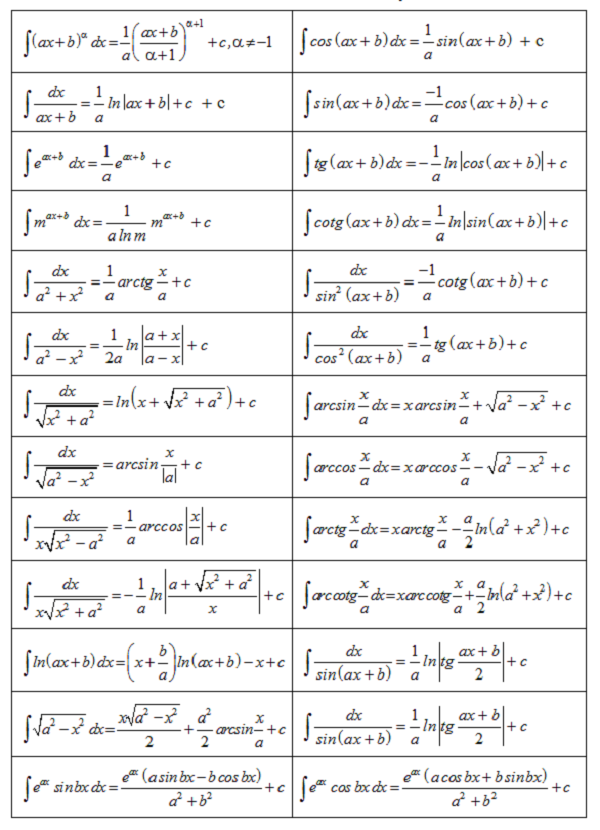
Bảng nguyên hàm và công thức nâng cao
=> Bảng nguyên hàm và các dạng công thức dạng nâng cao đầy đủ mọi người xem có thể tải ảnh về học thuộc để áp dụng vào giải bài tập.

Hy vọng với chia sẻ thông tin về bảng nguyên hàm cũng như các công thức nguyên hàm từ cơ bản đến nâng cao cũng như nguyên hàm mở rộng sẽ giúp các bạn có được nhiều thông tin kiến thức để áp dụng vào học và làm giải các bài tập.




