Công thức tính diện tích tam giác vuông, đều, cần kèm VD có lời giải

Diện tích tam giác là kiến thức được học từ lớp 5 tiểu học nhưng lại là kiến thức quan trọng được áp dụng xuyên suốt trong quá trình học toán từ cấp 2 lên cấp 3. Không những thế, ở các bài kiểm tra hay các đề thi cao đẳng, đại học có bài tập cần sử dụng công thức tính diện tích tam giác. Chính vì vậy, Huyndai Smart Phone sẽ chia sẻ công thức tính diện tích tam giác vuông, cân, đều kèm theo các dạng bài tập có lời giải để các bạn cùng củng cố lại kiến thức của mình nhé.

Công thức tính diện tích tam giác thường

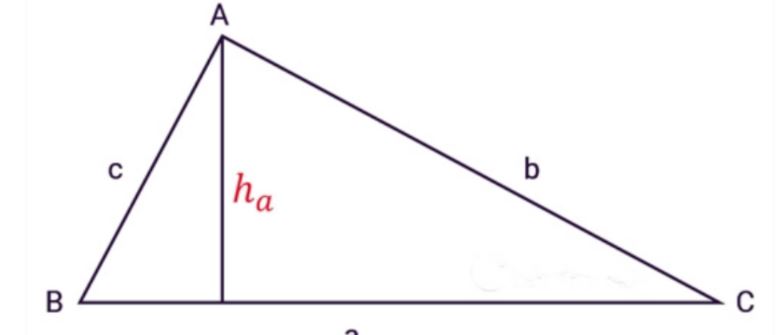
Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác, diện tích tam giác thường sẽ bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.

S = ½ h.a

Trong đó:

• S: là diện tích tam giác
• a: độ dài cạnh đáy
• h: chiều cao hạ từ đỉnh xuống đáy a

Ví dụ 1: Tính diện tích tam giác ABC biết độ dài cạnh đáy BC = 4 cm, độ dài đường cao kẻ từ đỉnh A bằng 16 cm. Tính diện tích tam giác ABC.

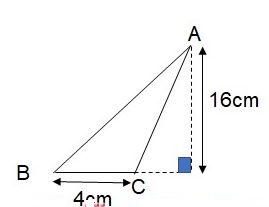
Lời giải

Tam giác ABC có đường cao nằm ngoài tam giác. Diện tích tam giác vẫn được tính theo công thức:

S_ABC = ½ h.a = ½.16.4 = 32 (cm²)

Ví dụ 2: Một tấm bảng quảng cáo hình tam giác có tổng cạnh đáy và chiều cao là 28m, cạnh đáy hơn chiều cao 12m. Tính diện tích tấm bảng quảng cáo đó ?

Lời giải:

Độ dài cạnh đáy là:

a = (28 + 12) : 2 = 20 (m)

Độ dài chiều cao là:

h = 28 – 20 = 8 (m)

Diện tích tấm bảng quảng cáo là:

S = ½ h.a = 20 x 8 : 2 = 80 (m²)

Đáp số: 80m²

Ví dụ 3: Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.

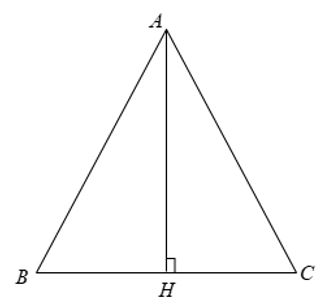
Lời giải

Xét Δ ABC cân tại A có AB = AC = b, BC = a.

Từ A kẻ AH ⊥ BC.

Ta có BH = HC = ½ BC = a/2

Khi đó ta có: SABC = ½AH.BC = ½.a.AH

Áp dụng định lý Py – to – go ta có:

AC² = AH² + HC² ⇒ AH = √ (AC² – HC²)

Tính diện tích tam giác khi biết một góc

Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.

S = ½a.b.sinCˆ  = ½a.c.sinBˆ = ½b.c.sin Aˆ

Ví dụ: Tam giác ABC có cạnh BC = 9, cạnh AB = 7, góc B bằng 60 độ. Tính diện tích tam giác ABC?

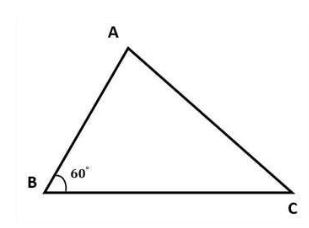
Lời giải

S = ½a.c.sinBˆ = ½. 9.7.sin60⁰ = (63√3)/4

Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron

Sử dụng công thức Heron đã được chứng minh:

S = √p(p-a)(p-b)(p-c)

Trong đó p là nửa chu vi tam giác:

p = ½ (a+b+c)

Công thức viết lại:

S = ¼√(a+b+c)(a+b-c)(b+c-a)(c+a-b)

Ví dụ: Tính diện tích hình tam giác có độ dài cạnh AB = 7, AC = 6, CB = 9

Lời giải:

Nửa chu vi tam giác ABC là

p = ½ (a+b+c) = (7 + 6 + 9) : 2 = 11 cm

Áp dụng công thức hero ta có:

S = √(p(p-AB)(p-AC)(a-BC)

= √11(11-7)(11-6)(11-9) = 2√110 cm²

Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R)

S_ABC = abc/4R = 2.R².sinAˆ.sinBˆ.sinCˆ

Trong đó:

• a, b, c: Độ dài cạnh của tam giác
• R: Bán kính đường tròn ngoại tiếp tam giác

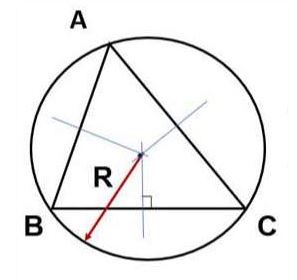
Lưu ý: các bạn cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.

Ví dụ: TCho tam giác ABC, độ dài các cạnh a = 4, b = 5, c = 3, R = 6 (R là bán kính đường tròn ngoại tiếp tam giác ABC). Tính diện tích của tam giác ABC.

Lời giải

S_ABC = abc/4R = (4.5.3) : (4.6) = 2,5

Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r)

S = p.r

Trong đó:

• S là điện tích tam giác
• p: Nửa chu vi tam giác.
• r: Bán kính đường tròn nội tiếp.

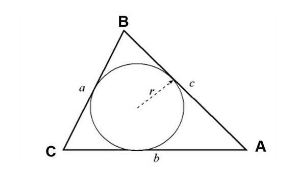
Ví dụ: Tính diện tích tam giác ABC biết độ dài các cạnh AB = 25, AC = 20, BC = 15, r = 6 (r là bán kính đường tròn nội tiếp tam giác ABC).

Lời giải

Nửa chu vi tam giác là:

p = (AB + AC + BC):2 = (25 + 20 + 15) :2 = 30

Diện tích tam giác là:

S = p.r = 30.6 = 180

Tham khảo thêm: Tập xác định của hàm số mũ, lũy thừa, logarit kèm VD có lời giải

Công thức tính diện tích tam giác vuông

Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.

S = ½a.b

Trong đó:

• S là diện tích tam giác vuông
• a, b là độ dài của hai cạnh góc vuông

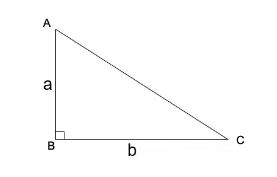
Ví dụ: Tính diện tích của tam giác vuông có:

a, Hai cạnh góc vuông lần lượt là 3cm và 4cm

b, Hai cạnh góc vuông lần lượt là 6m và 8m

Lời giải:

a, Diện tích của hình tam giác là:

(3 x 4) : 2 = 6 (cm²)

Đáp số: 6cm²

b, Diện tích của hình tam giác là:

(6 x 8) : 2 = 24 (m²)

Đáp số: 24m²

Công thức tính diện tích tam giác vuông cân

Diện tích tam giác vuông cân bằng ½ bình phương cạnh đáy S = ½a² .Trong đó a là chiều cao và cạnh đáy bằng nhau

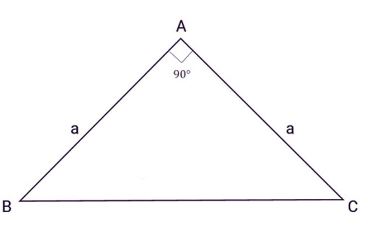
Ví dụ: Cho tam giác ABC vuông cân tại A, có AB = AC = 6cm. Tính diện tích tam giác ABC.

Lời giải:

Do cạnh AB = AC = a = 6cm

Xét tam giác ABC vuông cân tại A, ta có:

S = ½a² = 6² : 2 = 18 cm²

Công thức tính diện tích tam giác đều

Tam giác đều có độ dài 3 cạnh đều bằng nhau và tất cả các góc trong tam giác đều bằng 60 độ. Do đó, diện tích tam giác đều được tính bằng công thức:

S = ½. a². sin 60^o = a² .√3/4

Trong đó

• S là diện tích tam giác
• a chính là cạnh của tam giác đều.

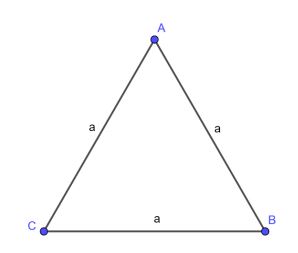
Ví dụ: Cho tam giác ABC đều các cạnh a = 6 cm. Tính diện tích tam giác.

Lời giải:

Áp dụng công thức tính S = ½. a². sin 60^o = ½.6². √3/4 = 9.√3/2 cm²

Công thức tính diện tích tam giác cân

Diện tích tam giác cân cũng giống như diện tích tam giác thường bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó

S = ½a.h_a

Trong đó:

• a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
• h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).

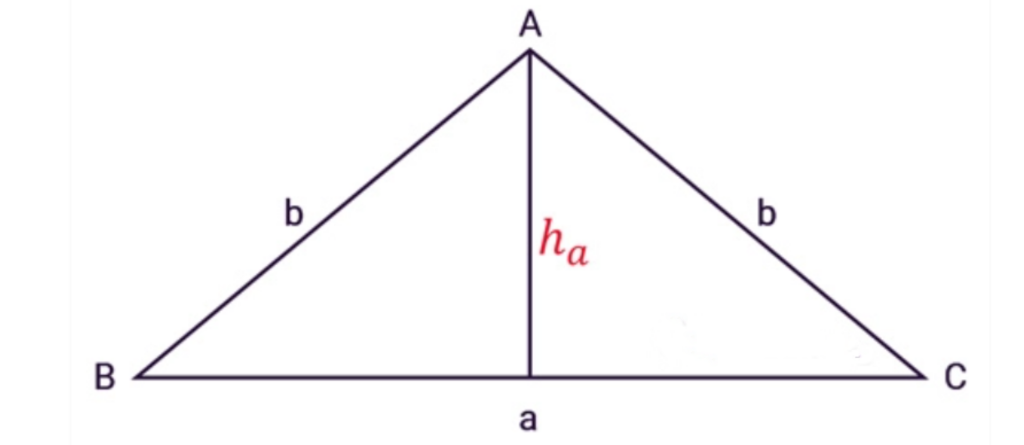
Ví dụ: Tính diện tích của tam giác cân có:

a, Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm

b, Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m

Lời giải:

a, Diện tích của hình tam giác là:

S = ½a.h_{a ⁼} (6 x 7) : 2 = 21 (cm²)

Đáp số: 21cm²

b, Diện tích của hình tam giác là:

S = ½a.h_{a ⁼} (5 x 3,2) : 2 = 8 (m²)

Đáp số: 8m²

Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn nhớ được các công thức tính diện tích tam giác vuông, cân, đều để vận dụng vào làm bài tập nhanh chóng và chính xác nhất.