Lý thuyết giá trị tuyệt đối và các dạng bài tập có lời giải từ A-Z

Hiện nay có rất nhiều các bạn học sinh không nắm chắc được kiến thức giá trị tuyệt đối là gì, tính chất của giá trị tuyệt đối, cách giải phương trình chứa dấu giá trị tuyệt đối và bất phương trình chứa dấu giá trị tuyệt đối như thế nào? Chính vì vậy, Hyundai Smart Phone sẽ chia sẻ lý thuyết giá trị tuyệt đối và các dạng bài tập có lời giải chi tiết để các bạn cùng tham khảo

Giá trị tuyệt đối là gì?

Giá trị tuyệt đối của một số hữu tỉ x là khoảng cách từ điểm x tới điểm O trên trục số, được kí hiệu là |x|

• Nếu x > 0 thì |x| = x.
• Nếu x = 0 thì |x| = 0.
• Nếu x < 0 thì |x| = -x.

Từ định nghĩa trên ta có thể viết như sau:

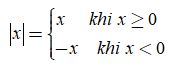
Ví dụ:

Nếu x = 4 thì |x| = |4| = 4.

Nếu x = -5 thì |x| = |-5| = -5.

Lưu ý: Với mọi x ∈ Q ta luôn có |x| ≥ 0, |x| = |-x|, |x| > x.

Tính chất của giá trị tuyệt đối

Giá trị tuyệt đối của số không âm là chính nó, giá trị tuyệt đối của số âm là số đối của nó.

• Nếu a ≥ 0 => |a| = a
• Nếu a < 0 => |a| = -a
• Nếu x – a ≥ 0 => |x-a| = x -a
• Nếu x – a ≤ 0 => |x-a| = a – x

Giá trị tuyệt đối của mọi số đều không âm |a| ≥ 0 với mọi a ∈ R

• |a| = 0 ⇔ a = 0
• |a| ≠ 0 ⇔ a ≠ 0

Hai số bằng nhau hoặc đối nhau thì giá trị tuyệt đối bằng nhau và ngược lại 2 số có giá trị tuyệt đối bằng nhau thì 2 số đó bằng nhau hoặc đối nhau.

• |a| = |b| => a = b hoặc a = – b

Mọi số đều lớn hơn hoặc bằng đối của giá trị tuyệt đối của nó và cũng nhỏ hơn hoặc bằng giá trị tuyệt đối của nó

• -|a| ≤ a ≤ |a| và -|a| = a => a ≤0, a = |a| => a ≥ 0

Trong 2 số âm dương số nào nhỏ hơn thì giá trị tuyệt đối sẽ lớn hơn. Nếu a < b < 0 => |a| > |b|

Trong 2 số dương số nào nhỏ hơn thì có giá trị tuyệt đối nhỏ hơn. Nếu 0 < a < b => |a| < |b|.

Giá trị tuyệt đối của một tích sẽ bằng tích các giá trị tuyệt đối: |a.b| = |a|. |b|

Giá trị tuyệt đối của một thương sẽ bằng thương hai giá trị tuyệt đối: |a/b| = |a/b|

Bình phương giá trị tuyệt đối của một số sẽ là bình phương số đó: |a|² = a²

Tổng giá trị tuyệt đối của 2 số luôn lớn hơn hoặc gần bằng giá trị tuyệt đối của 2 số, dấu xảy ra khi 2 số cùng dấu: |a| + |b| ≥ |a+b| và |a| +|b| = |a+b| => ab ≥ 0

Phương trình chứa dấu giá trị tuyệt đối

Phương trình chứa dấu giá trị tuyệt đối là phương trình có chứa ẩn trong dấu giá trị tuyệt đối.

1. Phương trình có dạng: |f(x)| = a; (a>0)

Cách giải : |f(x)| = a;(a>0)⇔ f(x) = a hoặc f(x) = −a

Ví dụ 1: |2x|=x−6

Ta có: |2x|=2x khi x≥0;

|2x|=−2x khi x<0.

– Với x≥0 ta có: |2x|=x−6⇔2x=x−6 ⇔x=−6

Giá trị x=−6 không thoả mãn điều kiện x≥0.

– Với x<0 ta có: |2x|=x−6⇔−2x=x−6 ⇔−3x=−6⇔x=2

Giá trị x=2 không thoả mãn điều kiện x<0.

Vậy phương trình vô nghiệm.

2. Phương trình có dạng : |f(x)| = |g(x)|

Cách giải : |f(x)| = |g(x)| ⇔ f(x) = g(x) hoặc f(x) = −g(x)

Ví dụ: Giải phương trình |x – 3| = |2 + 2x|

Lời giải:

Tham khảo thêm: Tập xác định của hàm số mũ, lũy thừa, logarit kèm VD có lời giải

Bất phương trình chứa dấu giá trị tuyệt đối

Bất phương trình chứa dấu giá trị tuyệt đối được hiểu là bất phương trình có chứa ẩn trong dấu giá trị tuyệt đối. Bất phương trình này có 3 dạng cơ bản là:

• |f(x)| > g(x) ⇔ f(x) > g(x) hoặc f(x) < −g(x)
• |f(x)| < |g(x)| ⇔ [f(x)]² < [g(x)]²
• |f(x)| < g(x) ⇔ −g(x) < f(x) < g(x)

Các dạng bài tập về giá trị tuyệt đối có lời giải

Dạng 1: |A(x)| = k (Trong đó A(x) là biểu thức chứa x, k là một số cho trước)

Cách giải:

• Nếu k < 0 thì không có giá trị nào của x thoả mãn đẳng thức (Vì giá trị tuyệt đối của mọi số đều không âm)
• Nếu k = 0 thì ta có |A(x)| = 0 → A(x) = 0
• Nếu k > 0 thì ta có: |A(x)| = k → A(x) = k hoặc A(x) = -k

Ví dụ : Tìm x biết

a. ∣2x − 3⁄2∣ = −½

b. 3⁄2 − ∣2x − 7⁄4∣ = 5⁄4

Lời giải

a. ∣2x − 3⁄2∣ ≥0 nên không có giá trị nào thỏa mãn ∣2x − 3⁄2∣ = −½

b. 3⁄2 − ∣2x − 7⁄4∣ = 5⁄4

⇔ ∣2x − 7⁄4∣ = 5⁄4 – 3⁄2

⇔ ∣2x − 7⁄4∣ = ¼

⇔ 2x − 7⁄4 = ¼ hoặc 2x − 7⁄4 = – ¼

⇔ x = 1 hoặc x = 3⁄4

Dạng 2: Phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = |Q(x)|

Phương pháp: Để tìm x trong bài toán dạng |A(x)| = |B(x)|, trong đó (A(x) và B(x) là biểu thức chứa x ta vận dụng tính chất sau:

|a| = |b| ⇔ a = b hoặc a = -b. Tức là |A(x)| = |B(x)| ⇔ A(x) = B(x) hoặc A(x) = -B(x)

Ví dụ: Tìm x biết

a) |5x – 4| = |2x + 3|

b) |x + 5| = |2x – 1|

Lời giải

a) | 5x – 4| = |2x + 3| ⇔ 5x – 4 = 2x + 3 hoặc 5x – 4 = -(2x + 3)

Trường hợp 1:

5x – 4 = 2x + 3 ⇔ 3x = 7 ⇔ x =  7⁄3

Trường hợp 2:

5x – 4 = -(2x + 3) ⇔ 7x = 1 ⇔ x = ¹⁄7

Vậy x =  7⁄3 và x = ¹⁄7 thỏa mãn điều kiện bài toán.

b) |x + 5| = | 2x – 1| ⇔ x + 5 = 2x – 1 hoặc x + 5 = -(2x – 1)

Trường hợp 1:

x + 5 = 2x – 1 ⇔ x = 6

Trường hợp 2:

x + 5 = -(2x – 1) ⇔ 3x = -4 ⇔ x = -4⁄3

Vậy x = 6 và x = -4⁄3 thỏa mãn điều kiện bài toán.

Dạng 3: Giải phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = Q(x)

Phương pháp: Để giải phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = Q(x) (trong đó P(x) và Q(x) là biểu thức chứ x) ta thực hiện 1 trong 2 cách sau

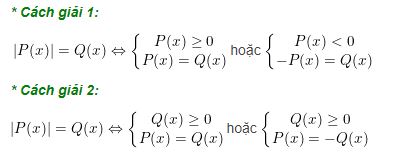
Ví dụ 1: Tìm nghiêm của phương trình sau:

a) |x + 3| = 1 – 2x

b) |2x – 5| = x

c) | −3x| = x −8

Lời giải

a) |x + 3| = 1 – 2x (*)

Trường hợp 1: x + 3 ≥ 0 ⇔ x ≥ -3

Phương trình (*) ⇔ x + 3 = 1 – 2x ⇔ 3x = -2 ⇔ x = -2⁄3 (thỏa mãn)

Trường hợp 2: x + 3 < 0 ⇔ x < -3

Phương trình (*) ⇔ x + 3 = -(1 – 2x) ⇔ x = 4 (không thỏa mãn)

Vậy nghiệm của phương trình là x = -2⁄3

b) |2x – 5| = x (**)

Trường hợp 1: x ≥ 0

Phương trình (**) ⇔ 2x – 5 = x ⇔ x = 5 ( thỏa mãn)

Trường hợp 2: x ≥ 0

Phương trình (**) ⇔ 2x – 5 = -x ⇔ 3x = 5 ⇔ x = 5⁄3 (thỏa mãn)

Vậy nghiệm của phương trình là x = 5 hoặc x = 5⁄3

c) | −3x| = x −8

Ta có:

|−3x| = −3x khi −3x ≥ 0 ⇔ x ≤ 0; |−3x| = 3x khi −3x < 0 ⇔ x > 0

– Với x ≤ 0 ta có:

|− 3x| = x − 8 ⇔ −3x = x − 8 ⇔ 4x = 8 ⇔ x=2

Giá trị x = 2 không thoả mãn điều kiện x ≤ 0

– Với x > 0 ta có:

|−3x| = x−8 ⇔ 3x  = x−8  ⇔ 2x = −8 ⇔ x = −4

Giá trị x = −4 không thoả mãn điều kiện x > 0.

Vậy phương trình vô nghiệm

Dạng 4: Giải phương trình chứa dấu giá trị tuyệt đối có dạng |A(x)| + |B(x)| = C(x)

Phương pháp giải: Để giải phương trình chứa dấu giá trị tuyệt đối có dạng |A(x)| + |B(x)| = C(x) (trong đó A(x), B(x), C(x) là các biểu thức chứa ẩn x) ta làm như sau:

• Bước 1: Xét dấu các biểu thức chứa ẩn x nằm trong dấu giá trị tuyệt đối.
• Bước 2: Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối.
• Bước 3: Dựa vào bảng xét dấu, chia từng khoảng để giải phương trình
• Bước 4: Đối chiếu nghiệm với các điều kiện tương ứng để chọn ra nghiệm thỏa mãn yêu cầu đề bài

Ví dụ: Giải phương trình sau: |x + 1| + | x – 2| = 2x + 3 (*)

Lời giải

Ta có |x + 1| = x + 1 khi x ≥ -1

|x + 1| = -x – 1 khi x < 1

|x – 2| = x – 2 khi x ≥ 2

|x – 2| = 2 – x khi x < 2

Từ đó ta có bảng sau:

Trường hợp 1: x < -1

Phương trình (*) ⇔ -2x +1 = 2x + 3 ⇔ 4x = -2

⇔ x = -½

( không thỏa mãn điều kiện x ≤ -1 )

Trường hợp 2: -1 ≤ x ≤ 3

Phương trình (*) trở thành: 3 = 2x + 3 ⇔ x = 0 ( thỏa mãn)

Trường hợp 3: x > 3

Phương trình (*) trở thành: 2x -1 = 2x – 3 ⇔ 0x = 2 ( vô lý )

Vậy phương trình có nghiệm duy nhất x = 0

Dạng 5: Giải phương trình chứa dấu giá trị tuyệt đối có dạng |A(x)| + |B(x)| = |A(x) + B(x)|

Phương pháp giải: Để giải phương trình chứa dấu giá trị tuyệt đối |A(x)| + |B(x)| = |A(x) + B(x)| ta dựa vào tính chất: |A(x) + B(x)| ≤ |A(x) + B(x)| nên phương trình tương đương với điều kiện xảy ra đẳng thức A(x).B(x) ≥ 0

Ví dụ: Giải phương trình sau:

|5x + 1| + |3 – 2x| = |4 + 3x|

Lời giải

Ta có

|4 + 3x| = |5x + 1| + |3 – 2x| ≤ |5x + 1| + |3 – 2x|, ∀x ∈ R

⇔-1⁄5 < x < 3⁄2 (vô lý)

Vậy -1⁄5 ≤ x ≤ 3⁄2

Ví dụ 2: Giải phương trình sau:

|x + 2| +| 3 – x| = 5

Lời giải

Ta có |x + 2| + |3 – x | ≥ |( x + 2) + (3 – x)| ∀x ∈ R

⇔ |x + 2| + |3 – x | ≥ 5

Dấu bằng xẩy ra khi và

chỉ khi (x + 2).(3 – x) ≥ 0

Ta có bảng xét dấu sau:

Từ bảng xét dấu suy ra (x + 2).(3 – x) ≥ 0 ⇔ -2 ≤ x ≤ 3

Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nắm chắc được kiến thức về giá trị tuyệt đối để vận dụng vào làm bài tập. Hãy thường xuyên theo dõi chúng tôi để được chia sẻ những kiến thức bổ ích khác về máy tính, công nghệ,..