Nếu bạn không biết cách tìm giới hạn của một hàm số như thế nào thì hãy đọc ngay bài viết của Hyundai Smart Phone sẽ được chia sẻ lý thuyết giới hạn của hàm số và các dạng bài tập về giới hạn hạn số có đáp án chi tiết trong bài viết này
Lý thuyết về giới hạn của hàm số
1. Giới hạn hữu hạn của hàm số tại một điểm
a. Định nghĩa
Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.
Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \ {x0} và xn → x0, ta có f(xn) → L.
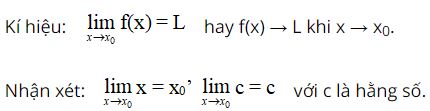
b. Định lí
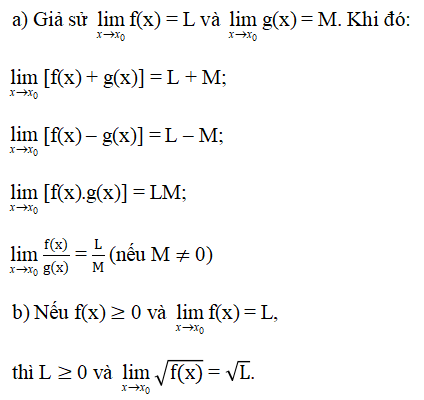
(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với x ≠ x0).
c. Giới hạn một bên
Cho hàm số y = f(x) xác định trên (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.
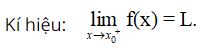
Cho hàm số y = f(x) xác định trên (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.
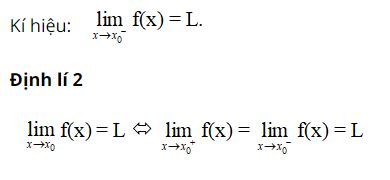
2. Giới hạn hữu hạn của hàm số tại vô cực
a) Cho hàm số y = f(x) xác định trên khoảng (a;+∞).
Ta nói hàm số y = f(x) có giới hạn là L khi x→+∞ nếu với dãy số (xn) bất kì, xn > a và xn→+∞, ta có f(xn)→L
b) Cho hàm số y = f(x) xác định trên khoảng (−∞;a).
Ta nói hàm số y = f(x) có giới hạn là L khi x→−∞ nếu với dãy số (xn) bất kì, xn < a và xn→−∞, ta có f(xn)→L.
3. Giới hạn vô cực của hàm số
a. Giới hạn vô cực
Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → –∞
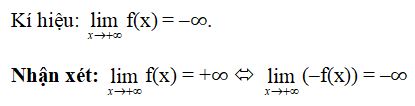
b. Một vài giới hạn đặc biệt
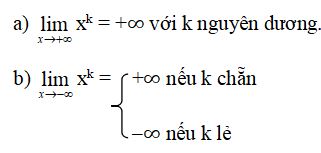
c. Một vài quy tắc về giới hạn vô cực
Quy tắc tìm giới hạn của tích f(x).g(x)
Quy tắc tìm giới hạn của thương f(x)/g(x)
(Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với x ≠x0). Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp:x→x0+, x→x0–; x→+∞; x→−∞.
THam khảo thêm:
- Phương trình parabol đi qua 2 điểm, 3 điểm, gốc tọa độ kèm VD
- Cách tính lim thủ công, máy tính đơn giản kèm theo VD từ A – Z
- Lý thuyết giá trị tuyệt đối và các dạng bài tập có lời giải từ A-Z
Các dạng bài tập giới hạn của hàm số có đáp án
1. Dạng 1: Tìm giới hạn của hàm số bằng định nghĩa
Phương pháp:
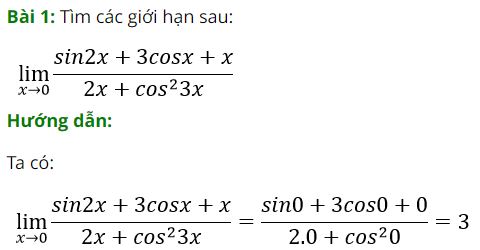
2. Dạng 2: Tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng
Tìm 
trong đó f(x0) = g(x0) = 0
Dạng này ta gọi là dạng vô định 0/0
Để khử dạng vô định này ta sử dụng định lí Bơzu cho đa thức:
Định lí: Nếu đa thức f(x) có nghiệm x = x0 thì ta có: f(x) = (x-x0)f1(x)
* Nếu f(x) và g(x) là các đa thức thì ta phân tích
f(x) = (x-x0)f1(x) và : g(x) = (x-x0)g1(x).
Khi đó 
, nếu giới hạn này có dạng 0/0 thì ta tiếp tục quá trình như trên.
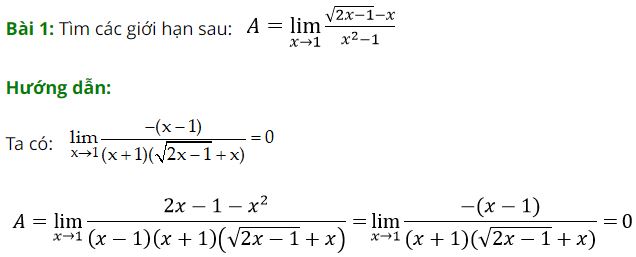
3. Dạng 3: Tìm giới hạn hàm số dạng 0 nhân vô cùng
Phương pháp: Tính giới hạn 
.
Ta có thể biến đổi 
về dạng 0/0 hoặc ∞/∞ rồi dùng các phương pháp tính giới hạn của hai dạng kia để làm.
Tuy nhiên, trong nhiều bài tập ta chỉ cần biến đổi đơn giản như đưa biểu thức vào trong (hoặc ra ngoài) dấu căn, quy đồng mẫu thức …. Là có thể đưa về dạng quen thuộc.
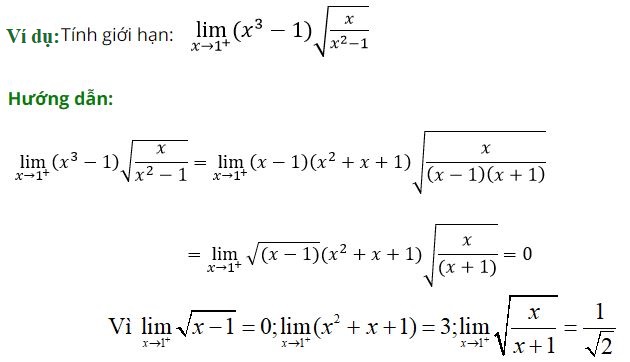
4. Dạng 4: Tìm giới hạn hàm số dạng vô cùng trừ vô cùng, vô cùng trên vô cùng
Phương pháp: Những dạng vô định này ta tìm cách biến đổi đưa về dạng ∞/∞
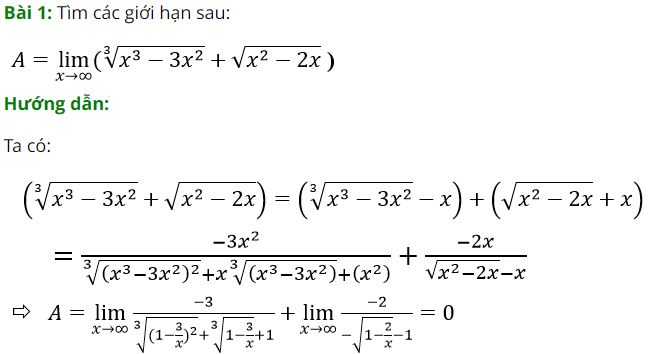
Bên trên chính là toàn bộ lý thuyết về giới hạn của hàm số và các dạng bài tập thường gặp trong quá trình học tập có thể giúp các bạn học sinh hệ thống lại kiến thức để áp dụng vào làm bài tập nhanh chóng và chính xác nhất.
