Hình chóp tam giác đều là gì? Tính chất, diện tích, thể tích hình chóp tam giác đều

Nếu các bạn muốn ôn lại kiến thức về hình chóp tam giác đều là gì thì hãy đọc ngay bài viết dưới đây của Hyundai Smart Phone sẽ được chia sẻ định nghĩa, tính chất, công thức tính diện tích xung quanh, toàn phần và thể tích hình chóp tam giác đều có bài tập minh họa chi tiết nhất

Hình chóp tam giác đều là gì?

Hình chóp tam giác đều là hình chóp có đáy là tam giác đều, các mặt bên (cạnh bên) đều bằng nhau hay hình chiếu của đỉnh chóp xuống đáy trùng với tâm của tam giác đều.

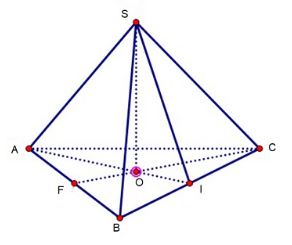
Tính chất hình chóp tam giác đều

• Đáy là tam giác đều
• Tất cả các cạnh bên bằng nhau
• Tất cả các mặt bên là các tam giác cân bằng nhau
• Chân đường cao trùng với tâm mặt đáy (Tâm đáy là trọng tâm tam giác ABC)
• Tất cả các góc tạo bởi cạnh bên và mặt đáy đều bằng nhau
• Tất cả các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau

Lưu ý:

• Tâm của tam giác đều là giao điểm 3 đường trung tuyến, cũng là đường cao, trung trực và phân giác trong.
• Tâm của hình vuông chính là giao điểm hai đường chéo.

Phân biệt chóp tam giác đều và tứ diện đều

Để phân biệt giữa hình chóp tam giác đều và hình chóp tứ giác đều ta sẽ dựa vào đặc điểm của mặt đáy để phân biệt cụ thể như sau:

• Hình chóp tam giác đều là hình chóp đều có đáy là tam giác (mặt bên là tam giác cân, chưa đều)
• Hình chóp tứ giác đều là hình chóp đều có đáy là tứ giác, lúc này đáy là hình vuông, mặt bên là tam giác cân.

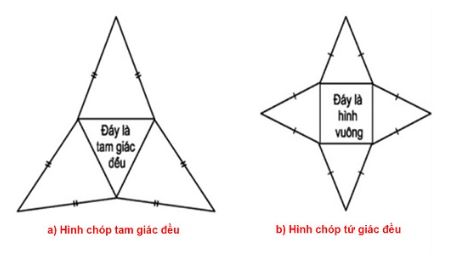
Cách vẽ hình chóp tam giác đều

Để vẽ hình chóp tam giác đều bạn thực hiện theo trình tự dưới đây:

• Bước 1: Vẽ mặt đáy hình chóp là tam giác đều ABC (không cần thiết phải vẽ 3 cạnh bằng nhau hoàn toàn mà có thể vẽ tam giác thường), đoạn AC vẽ nét đứt.
• Bước 2: Vẽ hai đường trung tuyến CF và AI giao nhau tại O, O chính là chân đường cao trùng với tâm đáy.
• Bước 3: Từ O, dựng đường thẳng đứng, ta được đỉnh S, từ S nối với đỉnh A, B, C. Ta có hình chóp tam giác đều SABCD với O là tâm đáy, SO là đường cao và SA = SB = SC

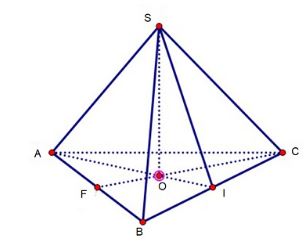
Công thức tính diện tích xung quanh hình chóp tam giác đều

S_xq = p×d

Trong đó:

• d là trung đoạn
• p là nửa chu vi đáy.
• Sxq: Diện tích xung quanh

Tham khảo thêm: Hình chữ nhật là gì? Tính chất, diện tích hình chữ nhật và bài tập từ A – Z

Công thức tính diện tích toàn phần hình chóp tam giác đều

Diện tích toàn phần của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng của diện tích xung quanh và diện tích đáy:

S_tp = S_xq + S_đáy

Trong đó:

• S_tp là diện tích toàn phần hình chóp tam giác đều
• S_đáy là diện tích đáy hình chóp tam giác đều
• S_xq là diện tích xung quanh hình chóp tam giác đều

Xem ngay: Hình thang cân là gì? Tính chất, chu vi, diện tích hình thang cân kèm VD

Công thức tính thể tích hình chóp tam giác đều

Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng 1⁄3 diện tích đáy nhân với chiều cao.

V = 1⁄3.h.S_đáy

Trong đó:

• V: Là thể tích hình chóp tam giác đều
• h: Là đường cao của hình chóp tam giác đều
• S_đáy: Diện tích đáy của hình chóp tam giác đều

Tham khảo thêm: Công thức tính thể tích khối trụ và bài tập có lời giải chuẩn 100%

Bài tập về hình chóp tam giác đều có đáp án

Ví dụ 1: Cho hình chóp tam giác đều S.ABC có thể tích là 100cm³; chiều cao của hình chóp là 3cm. Tính độ dài cạnh đaý?

Thể tích của hình chóp đều là:

V = 1⁄3.h.S_đáy ⇒S_đ = 3V/h = (3.1000):3 = 100 cm²

Gọi độ dài cạnh đáy là a.

Do đáy là tam giác đều nên diện tích đáy là:

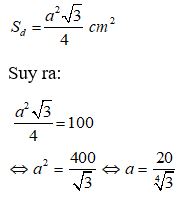
Ví dụ 2: Cho hình chóp tam giác đều S.ABC có các mặt là các tam giác đều. Gọi SH là đường cao của hình chóp, HC= 2√3 cm. Tính AB

Lời giải

Gọi M là giao điểm của CH và AB ta có CM AB và AM = BM.

Vì H là trọng tâm ΔABC nên:

CM = 3⁄2CH = 3⁄2.2√3  = 3√3 cm

Đặt AB = BC = x, ta có BC² – MB² = CM² (định lý Pytago cho ΔMBC) nên

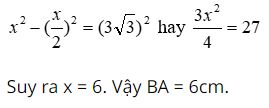
Ví dụ 3: Tính diện tích xung quanh của hình chóp tam giác đều có độ dài cạnh đáy là 10 cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là 12 cm.

Lời giải

a) Diện tích xung quanh của hình chóp tam giác đều là:

S_xq = [(10.3)/2].12 = 180 cm²

Ví dụ 4: Cho hình chóp tứ giác đều có các mặt bên là tam giác đều cạnh 4cm. Tính diện tích toàn phần của hình chóp?

Lời giải

Do mặt bên của hình chóp là tam giác đều cạnh 4cm nên đáy là hình vuông cạnh 4cm

Nửa chu vi đáy là

P = (4+4+4+4)/2 = 8cm

Các mặt bên là tam giác đều cạnh 4cm nên độ dài trung đoạn là

d = 4√3/2 = 2√3 cm

Diện tích xung quanh là:

S_xq = p.d = 8.2√3 = 16√3 cm²

Diện tích đáy là 4² = 16cm²

Diện tích toàn phần là

S^tp= 16√3 +16 cm²

Ví dụ 5: Cho khối chóp tam giác đều S. ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S. ABC.

Lời giải

Gọi O là trọng tâm tam giác ABC suy ra SO⊥ (ABCD).

Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC, khi đó AI là đường cao của tam giác đáy.

Ta có: BC = a nên BI = a⁄2.

Áp dụng định lý Pytago trong tam giác vuông ABI ta có:

Vậy thể tích khối chóp S. ABC là:

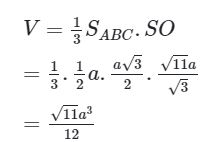
Ví dụ 6: Cho hình chóp đều S.ABC. Chứng minh rằng: Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện, mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.

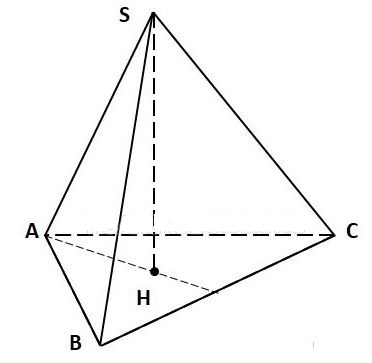
Lời giải

S.ABC là hình chóp đều

⇒ △ABC là tam giác đều ⇒ SA = SB = SC.

Do đó khi ta vẽ SH ⊥ (ABC)

⇒ H là trọng tâm của △ABC đều và có AH ⊥ BC.

Theo định lý ba đường vuông góc ⇒ SA ⊥ BC

Chứng minh tương tự ta được SB ⊥ AC và SC ⊥ AB.

Vì BC ⊥ AH và BC ⊥ SH ⇒ BC ⊥ (SAH)

Chứng minh tương tự ta có CA ⊥ (SBH) và AB ⊥ (SCH).

Bên trên chính là toàn bộ kiến thức về hình chóp tam giác đều là gì mà chúng tôi đã phân tích chi tiết có thể giúp các bạn nắm được tính chất và công thức tính diện tích xung quanh, toàn phần và thể tích hình chóp tam giác đều để vận dụng vào làm bài tập