Tập xác định của hàm số mũ, lũy thừa, logarit kèm VD có lời giải

Trong các bài kiểm tra hay đề thi có rất nhiều bài toán yêu cầu tìm tập xác định của hàm số mũ, lũy thừa, logarit nhưng có rất nhiều các bạn học sinh không làm được. Chính vì vậy, Hyundai Smart Phone sẽ hướng dẫn các bạn tìm tập xác định của hàm số logarit, lũy thừa, mũ kèm theo ví dụ để các bạn cùng tham khảo.

Tập xác định của hàm số mũ

Đối với hàm số mũ y=a^x(a > 0; a ≠ 1) thì không có điều kiện. Nghĩa là tập xác định của nó là R. Nên khi bài toán yêu cầu tìm tập xác định của hàm số mũ y=a^f(x)(a > 0; a ≠ 1) ta chỉ cần tìm điều kiện để f(x) có nghĩa (xác định)

Ví dụ 1: Tìm tập xác định D của hàm số y=(x²-1)^-8

Hướng dẫn:

Hàm số xác định khi và chỉ khi x²-1 ≠ 0 ⇔ x ≠ ±1

Ví dụ 2: Tìm tập xác định của các hàm số sau:

Lời giải

a. y = x³ vì 3 là số nguyên dương nên tập xác định của hàm số là: D = R

b. y = x^¹⁄3  vì ¹⁄3 là số hữu tỉ, không nguyên nên tập xác định của hàm số là D = (0, +∞ )

c. y = x^-√3 vì -√3 là số vô tỉ, không nguyên nên tập xác định của hàm số là: D = (0, +∞ )

d. y = e^{√2×2 – 8}

Điều kiện xác định của hàm số

2x² – 8 ≥ 0 ⇔ x ∈ (-∞, -4] ∪ [4, +∞)

Vậy tập xác định của hàm số: D = R\ (-4, 4 )

Tìm tập xác định của hàm số lũy thừa

Hàm số lũy thừa là các hàm số dạng y = x^α (α ∈ R). Các hàm số lũy thừa có tập xác định khác nhau, tùy theo α:

• Nếu α nguyên dương thì tập các định là R
• Nếu α nguyên âm hoặc α = 0 thì tập các định là R∖{0}
• Nếu α không nguyên thì tập các định là (0; +∞).

Lưu ý:

• Hàm số y = √x có tập xác định là [0; +∞).
• Hàm số y = ³√x có tập xác định R, trong khi đó các hàmy = x^½, y = x ^¹⁄3 đều có tập xác định (0; +∞).

Ví dụ 1: Tìm tập xác định của hàm số: y = (2x² – x -6)^-2

Lời giải

Điều kiện xác định của hàm số: 1 – x ≥ 0 ⇒ x ≤1 ⇒ D = R\(1,+∞)

Ví dụ 2: Tìm tập xác định của hàm số lũy thừa sau:

a) y=(1−x)^−¹⁄3
​
b) y=(2−x²)^³⁄5
​
c) y=(x²−1)⁻²

d) y=(x²−x−2)^√2

Lời giải

a) Hàm số y = (1−x)^−¹⁄3 xác định ⇔1−x > 0 ⇔ x < 1

Vậy tập xác định D = (−∞;1)

b, Hàm số y=(2−x²)^³⁄5 xác định định ⇔2−x² > 0 ⇔ x² < 2 ⇔ −2 ​< x < 2

Vậy tập xác định D=(−2​;2)

c,Hàm số y=(x²−1)⁻² xác định ⇔ x² −1≠0 ⇔ x² ≠ 1⇔x ±1

Vậy tập xác định D= R\{−1;1}.

d) Hàm số y=(x²−x−2)^√2 xác định ⇔x²−x−2 > 0⇔ (x+1)(x−2) > 0 ⇔ x<−1 hoặc x>2

Vậy tập xác định D=(−∞;−1)∪(2;+∞).

Ví dụ 3: Tìm tập xác định D của hàm số

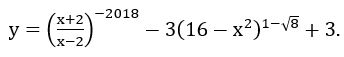
Hàm số xác định khi và chỉ khi

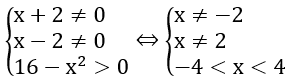
Vậy tập xác định của hàm số là D=(-4 ; 4)\{-2 ,2}.

Tìm tập xác định của hàm số logarit

Hàm số logarit y=log_ax, (a > 0; a ≠ 1) có tập xác định D = (0; +∞)

Hàm số logarit y=log_af(x), (a > 0; a ≠ 1) có điều kiện xác định là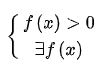

Hàm số y = log_g(x)f(x), (g(x) > 0; g(x) ≠ 1) có điều kiện xác định là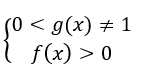

Hàm số y = (f(x))^g(x) xác định ⇔ f(x) > 0

Ví dụ 1: Tìm tập xác định của hàm số: y log₂(√x-2)

Lời giải

Điều kiện xác định của hàm số là

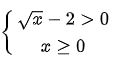
⇒x >1 ⇒D = (1,+∞)

Ví dụ 2: Tìm điều kiện xác định của hàm số: log₂(x²-5x+6)

Lời giải

Điều kiện xác định của hàm số: x²-5x+6 > 0 ⇒ x ∈(-∞,2)∪(3,+∞)

Ví dụ 3: Tìm tập xác định của hàm số y = (x²-16)^-5 – ln(24-5x-x²)

Hướng dẫn:

Tập xác định của hàm số y = (x²-16)^-5 – ln(24-5x-x²) là:

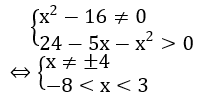
Vậy tập xác định là : D=(-8;3)\{-4}.

Ví dụ 4: Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=log₂(4x-2x+m) có tập xác định D=R.

Lời giải:

Hàm số có tập xác định D = R khi 4x – 2x + m > 0, (1), ∀x ∈ R

Đặt t = 2x, t > 0

Khi đó (1) trở thành t2 – t + m > 0 ⇔ m > – t² + t, ∀ t ∈ (0;+∞)

Đặt f(t) = -t² + t

Lập bảng biến thiên của hàm f(t) = -t² + t trên khoảng (0;+∞)

Yêu cầu bài toán xảy ra khi

Ví dụ 5: Tìm tập xác định của hàm số

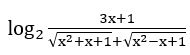
Lời giải

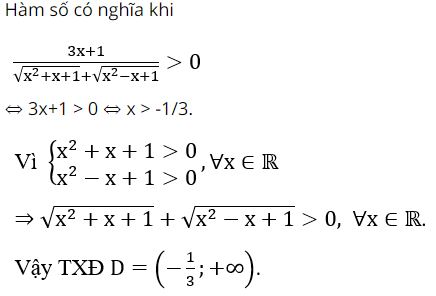
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn tìm được tập xác định của hàm số mũ, lũy thừa, logarit chính xác rồi nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi.