Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số và bài tập có đáp án

Trong môn toán lớp 12, các bạn học sinh cần nắm được định nghĩa và cách tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số thì mới có thể áp dụng được vào làm bài tập. Chính vì vậy, Hyundai Smart Phone sẽ tổng hợp lý thuyết về giá trị nhỏ nhất, giá trị lớn nhất của hàm số và các dạng bài tập trong bài viết dưới đây để các bạn cùng tham khảo

Định nghĩa giá trị nhỏ nhất, giá trị lớn nhất

Cho hàm số y = f(x) xác định trên miền D

Số M gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) ≤ M với mọi x thuộc D và tồn tại x₀ ∈ D sao cho f(x₀) ≤ M. Kí hiệu:

Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) ≥ m với mọi x thuộc D và tồn tại x₀ ∈ D sao cho f(x0) ≥ m. Kí hiệu:

Hay nói cách khác:

Tham khảo thêm:

• Lý thuyết giới hạn của hàm số và các dạng bài tập có đáp án chuẩn 100%
• Tìm m để hàm số đồng biến, nghịch biến trên khoảng kèm VD
• Phương trình parabol đi qua 2 điểm, 3 điểm, gốc tọa độ kèm VD

Các dạng bài tập tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số

1. Dạng 1: Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên một đoạn [a,b]

Phương pháp:

• Bước 1: Tìm tập xác định (nếu đề bài không cho sẵn)
• Bước 2: Tính f'(x) và giải phương trình f'(x) = 0 ⇒ x₁, x₂, x₃,….
• Bước 3: Tính f(x₁), f(x₂), f(x₃),….và f(a), f(b)
• Bước 4: So sánh và kết luận.

Ví dụ 1: Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x³ – 3x² – 9x + 2 trên đoạn [-2; 2].

Lời giải

Ta có: y’ = 3x² – 6x – 9 = 0

⇔

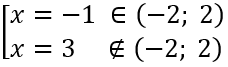
Mà y(-2) = 0; y(2) = -20; y(-1) = 7.

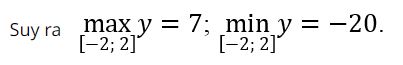
Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x – sin⁡2x trên đoạn [π/2; π]

Lời giải

Ta có y’ = 1 – 2cos2x = 0

⇔ cos2x = 1⁄2 = cos π/3

⇔ x = ±π/6 + kπ.

Xét x ∈ [(-π)/2; π] ta được x = ±π/6; x = 5π/6.

f((-π)/2) = -π/2; f(π) = π; f((-π)/6) = -π/6 + √3⁄2; f(π/6) = π⁄6 – √3⁄2; f(5π/6) = 5π/6 + √3⁄2.

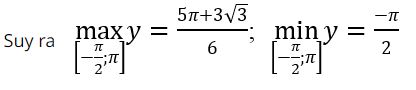
2. Dạng 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập D bất kì

Phương pháp:

• Bước 1: Tìm tập xác định (Nếu đề bài không cho sẵn tìm trên miền nào)
• Bước 2: Tính f'(x) và giải phương trình f'(x) = 0 ⇒ x₁, x₂, x₃,….
• Bước 3: Lập bảng biến thiên
• Bước 4: Dựa vào bảng biến thiên để kết luận.

Ví dụ 1: Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) = |x| + 3 trên [-1; 1]

Lời giải:

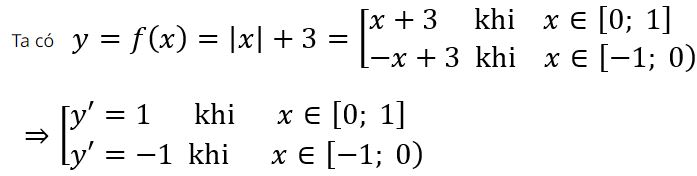
Ta có bảng biến thiên của hàm số đã cho.

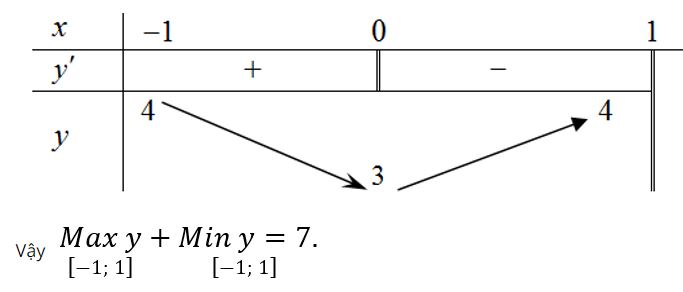
Ví dụ 2: Tìm giá trị nhỏ nhất của hàm số y = x + 4/x (x > 0)

Lời giải

Ta có: y’ = 1 – 4/x²

⇔ y’ = 0 ⇔1 – 4/x² = 0

⇔ x² – 4 = 0

⇔

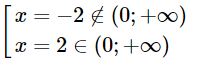
Bảng biến thiên:

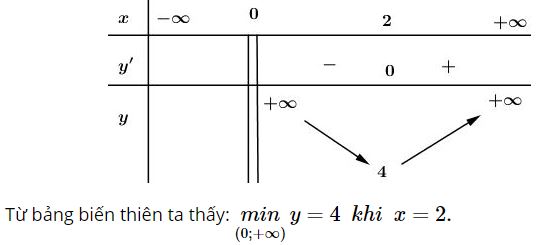
3. Dạng 3: Tìm m để hàm số có Giá trị lớn nhất, Giá trị nhỏ nhất thoả mãn điều kiện

• Bước 1: Tính f'(x) và giải phương trình f'(x) = 0 ⇒ x₁, x₂, x₃,….
• Bước 2: Tính f(x₁), f(x₂), f(x₃),….và f(a), f(b)
• Bước 3: Biện luận theo tham số để tìm GTLN, GTNN của hàm số trên đoạn [a,b]

Ví dụ 1: Tìm giá trị lớn nhất nhỏ nhất của hàm số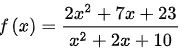

Lời giải

Dễ thấy x² + 2x + 10 > 0 ∀x nên hàm số xác định trên toàn trục số.

Gọi m là một giá trị tùy ý của hàm số, khi đó phương trình

2x² + 7x + 23/x² + 2x + 10 = m

⇔2x² + 7x + 23 = m(x² + 2x + 10)

⇔ (m-2)x² + (2m – 7)x + 10m – 23 = 0

Ta xét hai trường hợp sau:

TH1: Nếu m = 2 phương trình trở thành -3x – 3 = 0 ⇔ x = -1 ⇒ vậy phương trình có nghiệm khi m = 2

TH2: Nếu m ≠ 2 khi đó phương trình bậc 2 có nghiệm khi và chỉ khi:

Δ = (2m – 7)² – 4(m-2)(10m – 23) ≥ 0

⇔ -36m + 144m – 135 ≥ 0

⇔ 3⁄2 ≤ m ≤ 5⁄2 ≠ 2

⇔ max f(x) = 5⁄2, min f(x) = 3⁄2

Ví dụ 2: Cho hàm số y = x+m/x-1 với m là tham số thực). Tìm các giá trị của m đề hàm số thỏa mãn

Lời giải

TXĐ: D = E\{1}. Ta có y’ = -1-m/(x-1)²

Trường hợp 1: Nếu -1-m < 0 ⇔ m > -1

Ta có y'<0 ∀x ∈ D

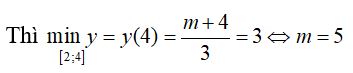
(thỏa mã điều kiện m >-1)

Trường hợp 2: Nếu -1-m > 0 ⇔ m <-1

Ta có y’ > 0 ∀x ∈ D thì:

(không thỏa mãn điều kiện m<-1)

Vậy m = 5

Bên trên chính là toàn bộ cách tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số mà chúng tôi đã phân tích chi tiết có thể giúp các bạn nắm chắc được kiến thức để vận dụng vào làm bài tập rồi nhé.