Trọng tâm là một trong những khái niệm quan trọng thuộc lĩnh vực toán học, vật lý và cả trong đời sống hàng ngày. Để tìm hiểu trọng tâm là gì? Cách xác định trọng tâm hay tính chất của trọng tâm như thế nào? Hi vọng bài viết dưới đây sẽ là nguồn tư liệu hữu ích, giúp các em củng cố kỹ năng giải toán để đạt được kết quả cao trong các bài kiểm tra, bài thi sắp tới.
Trọng tâm là gì?
Trọng tâm của một vật thể là điểm mà khi đặt một trụ thẳng đứng vào điểm đó, vật thể có thể đứng cân bằng.
Trọng tâm trong tam giác là giao điểm của 3 đường trung tuyến có tâm điểm của hình tam giác đó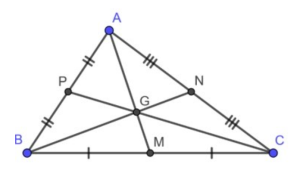
Tính chất trọng tâm trong tam giác
- Khoảng cách từ trọng tâm tới 3 đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Tính chất trọng tâm trong tam giác vuông
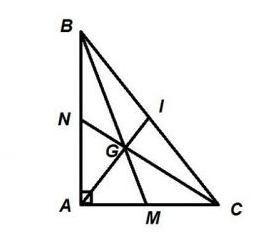
Trọng tâm của tam giác vuông cũng được xác định giống như trọng tâm của tam giác thường.
Tam giác MNP vuông tại M. 3 đường trung tuyến MD, NE, PF giao nhau tại trọng tâm O. Ta có MD là trung tuyến của góc vuông PMN nên MD = 1/2 PN = DP = DN.
Tham khảo ngay: Hình thang vuông là gì? Tính chất, Công thức tính chu vi, diện tích hình thang vuông
Tính chất trọng tâm trong tam giác cân
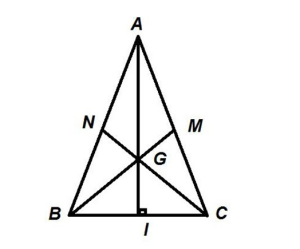
Tam giác ABC cân tại A, có G là trọng tâm.
Vì tam giác ABC cân tại A nên AG vừa là đường trung tuyến, đường cao và là đường phân giác, từ đó ta suy ra được hệ quả của trọng tâm tam giác cân ABC như sau:
- Góc BAD bằng góc CAD.
- Trung tuyến AD vuông góc với cạnh đáy BC.
Tính chất trọng tâm trong tam giác vuông cân
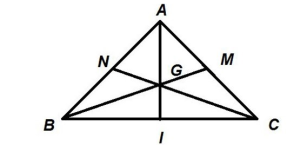
Có tam giác ABC vuông cân tại A và I là trọng tâm. AM là đường trung trực, đường trung tuyến và đường cao của tam giác này nên AM vuông góc với BC.
Mặt khác, vì tam giác ABC vuông cân tại A nên:
AB = AC.
⇒ BP = CN và BN = AN = CP = AP.
Tính chất trọng tâm trong tam giác đều
Tam giác ABC đều, G là giao điểm ba đường trung tuyến, đường cao, đường phân giác.
Vì vậy theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
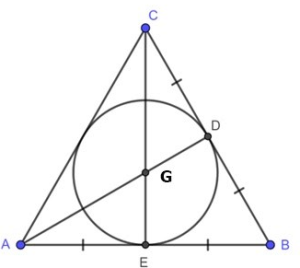
Cách xác định trọng tâm trong tam giác
Cách 1: Dựa vào khái niệm trọng tâm tam giác là giao điểm 3 đường trung tuyến, ta xác định trọng tâm tam giác bằng cách lấy giao điểm của ba đường trung tuyến.
- Vẽ tam giác ABC, lần lượt xác định trung điểm của các cạnh AB, BC, CA.
- Nối lần lượt các đỉnh đến trung điểm của cạnh đối diện. Nối A với G, B với F, C với E.
- Giao điểm I của ba đường trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.
- Xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến.
cách 2: Dựa vào tính chất về tỉ lệ các đoạn trên đường trung tuyến, ta xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến
- Vẽ tam giác ABC, xác định trung điểm M của cạnh BC.
- Nối đỉnh A với trung điểm M, sau đó lấy điểm S sao cho AS = 2/3 AM.
- Theo tính chất trọng tâm tam giác thì điểm S chính là trọng tâm tam giác ABC.
Xem ngay: Định nghĩa, tính chất, công thức tính đường trung tuyến kèm VD
Các dạng bài tập về trọng tâm trong tam giác có lời giải
Bài 1: Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.
Lời giải:
Gọi trung điểm MN, MP, PN lần lượt là R, O, S.
Khi đó MS, PR, NO đồng quy tại trọng tâm I.
Ta có ∆MNP đều, suy ra:
MS = PR = NO (1).
Vì I là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
MI = 2/3 MS, PI = 2/3 PR, NI = 2/3 NO (2).
Từ (1) , (2) ⇒ GA = GB = GC.
Bài 2: Tam giác ABC có trung tuyến AD = 9cm và trọng tâm I. Tính độ dài đoạn AI?
Lời giải:
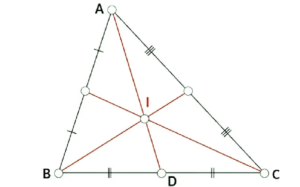
Ta có I là trọng tâm của tam giác ABC và AD là đường trung tuyến nên AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác).
Do đó: AG = (2/3).9 = 6 (cm).
Vậy đọan AI có độ dài 6 cm
Ví dụ 3: cho tam giác ABC có G là trọng tâm. Xác định điểm M sao cho:
![]()
A. Điểm M là trung điểm cạnh AC
B. Điểm M là trung điểm cạnh GC
C. Điểm M chia đoạn AB theo tỉ số 4
D. Điểm M chia đoạn GC thỏa mãn GC– = 4GM–
Lời giải
Do G là trọng tâm tam giác ABC và M là một điểm bất kỳ

Suy ra G, M, C thẳng hàng và M khác trung điểm của AB (2)
Vậy M chia đoạn GC thỏa mãn GC– = 4GM– ⇒ D đúng.
Từ (1) suy ra M khác trung điểm của GC (vì nếu M là trung điểm của GC thì GC– = 2GM– mâu thuẫn (1))⇒ B sai.
Từ (2) suy ra A và C sai vì A, M, C không thẳng hàng, do đó M không thể là trung điểm AC và A, M , B không thẳng hàng nên M không thể chia AB theo tỷ số 4.
Sau khi đọc song bài viết của chúng tôi có thể giúp các bạn biết được trọng tâm là gì, tính chất, công thức tính trọng tâm tam giác để áp dụng vào làm bài tập nhanh chóng và chính xác




