Hiện nay trên thế giới đa số còn rất nhiều các bạn hộc sinh còn chưa nắm chắc được các kiến thức cơ bản như ước chung lớn nhất là gì? Cách tìm ước chung lớn nhất như thế nào. Chính vì vậy, Hyundai Smart Phone sẽ giúp bạn biết và hiểu được thêm về lý thuyết ước chung lớn nhất và các dạng bài tập có lời giải chi tiết các bạn cùng tham khảo nhé.
Ước chung lớn nhất là gì?
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó. Ký hiệu là ƯCLN(a,b).
Ví dụ: Tìm ƯCLN(24, 16, 32)
Ư(24) = {1, 2, 3, 4, 6, 8, 12, 24}
Ư(16) = {1, 2, 4, 8, 16}
Ư(32) = {1, 2, 4, 8, 16, 32}
Vậy ƯCLN(24, 16, 32) = 8
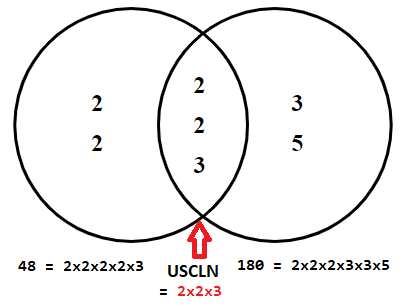
Cách tìm ước chung lớn nhất chi tiết nhất
1. Phân tích các số ra thừa số nguyên
- Bước 1. Phân tích các số ra thừa số nguyên tố
- Bước 2. Chọn ra các thừa số chung
- Bước 3. Lập tích các thừa số đã chọn ra. Mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
Ví dụ: Tìm ƯCLN(12, 30)
12 = 2 x 2 x 3
30 = 2 x 3 x 5
Ta có: các thừa số nguyên tố chung là 2 và 3.
Vậy ƯCLN(12, 30) = 2 x 3 = 6
2. Liệt kê các ước chung của các số rồi chọn ra ƯCLN
Ước chung lớn nhất của các số, ta tìm tập hợp các ước của từng số đó. Sau đó chọn ước chung lớn nhất.
Ví dụ: Tìm Ước chung lớn nhất của hai số tự nhiên 16 và 30.
Đầu tiên ta tìm tập hợp các ước của 16 và 30.
Ư(15) = { 1, 2, 4 , 8, 16 }
Ư(30) = { 1 , 2 , 3 , 5 , 6 , 10 , 15 , 30 }
Vậy ƯCLN (16,30) = 2
3. Tìm ƯCLN bằng bội chung nhỏ nhất (BCNN) (điều kiện a, b khác 0)
Ước chung lớn nhất của a và b có thể tính bằng cách lấy tích của a và b chia cho bội chung nhỏ nhất (BCNN) của a và b.
Ví dụ: Tìm ƯCLN(12, 30)
B(12) = {0, 12, 24, 36, 48, 60,…}
B(30) = {0, 30, 60,…}
Ta có: BCNN(12,30) = 60
Vậy ƯCLN(12,30) = 12.30:60 = 6
4. Sử dụng thuật toán Ơclit
Bước 1: Lấy số lớn chia số nhỏ, giả sử a = b . x + r
+ Nếu r ≠ 0 ta thực hiện bước 2
+ Nếu r = 0 thì ƯCLN(a, b) = b
Bước 2: Lấy số chia, chia cho số dư. B = r . y +r1
+ Nếu r1 ≠ 0 ta thực hiện bước 3
+ Nếu r1 = 0 thì ƯCLN(a, b) = r
Bước 3: Quá trình này được tiếp tục cho đến khi được một phép chia hết
Tham khảo thêm: Bội chung nhỏ nhất là gì? Cách tìm bội chung nhỏ nhất có VD kèm theo lời giải
Các dạng bài tập về ước chung lớn nhất có lời giải
1. Dạng 1: Tìm ước chung lớn nhất của các số cho trước
Cách 1: Để tìm ƯCLN của các số cho trước ta thực hiện quy tắc 3 bước phía trên.
a chia hết cho b => ƯCLN (a; b)
a chia b dư r thì ƯCLN (a; b) = ƯCLN (b; r)
Cách 2: Sử dụng thuật toán Ơ-clit
Bước 1: Lấy số lớn chia số nhỏ. Giả sử a = bx + r
- Nếu r # 0 ta thực hiện bước 2
- Nếu r = 0 thì ƯCLN (a; b) = b
Bước 2: Lấy số chia, chia cho số dư
- Nếu r1 # 0 ta thực hiện bước 3
- Nếu r1 = 0 thì ƯCLN (a; b) = b
Bước 3. Quá trình này được tiếp tục cho đến khi được một phép chia hết
Bài 1: Tìm ƯCLN(24, 30)
Lời giải
Số lớn nhất trong tập hợp ƯC(24,30) vừa tìm được là số 6.
Vậy ƯCLN(24, 30) = 6.
Bài 2: Tìm ƯCLN(18, 30).
Lời giải:
Ư(18) = {1; 2; 3; 6; 9; 18}
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
Do đó:
ƯC(18, 30) = {1; 2; 3; 6}
Số lớn nhất trong tập ƯC(18, 30) là 6.
Vậy ƯCLN(18, 30) = 6.
Bài 3: Tìm ƯCLN(18, 30).
Lời giải:
Ư(18) = {1; 2; 3; 6; 9; 18}
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
Do đó:
ƯC(18, 30) = {1; 2; 3; 6}
Số lớn nhất trong tập ƯC(18, 30) là 6.
Vậy ƯCLN(18, 30) = 6.
Bài 4: Tìm 2 số tự nhiên a và b. Biết a > b và tổng của 2 số bằng 500 và UCLN (a;b)=100
UCLN(a;b)=100
a=100m; b=100n
(m;n)=1 và m > n
a+b = 100m +100n =500
100(m+n) =500
m+n =5
m=3 và n=2 → a=300;b=200
M=4 và n=1 → a=400;b=100
Bài 5. Tìm ước chung lớn nhất của các số
a. ƯCLN (18; 30)
b. ƯCLN (24; 48)
c. ƯCLN (18; 30; 15)
d. ƯCLN (24; 48; 36)
Lời giải:
a. ƯCLN (18; 30)
Phân tích các số ra thừa số nguyên tố
18 = 2 . 32
30 = 2 . 3 . 5
Từ đó ƯCLN (18; 30) = 2 . 3 = 6
b. Phân tích các số ra thừa số nguyên tố
24 = 23 . 3
48 = 24 . 3
Từ đó ƯCLN (24; 48) = 23 . 3. = 24
c. 18 = 2 . 32
30 = 2 . 3 . 5
15 = 3 . 5
ƯCLN (18; 30; 15) = 3
d. 24 = 23 . 3
48 = 24 . 3
36 = 22 . 32
Từ đó ƯCLN (24; 48; 36) = 22 . 3 = 12
Bài 6: Sử dụng thuật toán Ơ-clit để tìm
a. ƯCLN (174; 18)
b. ƯCLN (124; 16)
Lời giải:
a. Ta thực hiện theo các bước:
Lấy 174 chia cho 18 ta được 174 = 9 . 18 + 12
Lấy 18 chia cho 12 ta được 18 = 1 . 12 + 6
Lấy 12 chia cho 6 ta được 12 = 2 . 6 + 0
Vậy ta được ƯCLN (174; 18) = 6
b. Ta thực hiện theo các bước:
Lấy 124 chia cho 16, ta được 124 = 7 .16 + 12
Lấy 16 chia cho 12, ta được 16 = 1 . 12 + 4
Lấy 12 chia cho 4 ta được 12 = 3 . 4 + 0
Vậy ƯCLN (124; 16) = 4
Bài 7: Tìm ƯCLN rồi tìm các ước chung của :
a) 16 và 24 ; b) 180 và 234 ; c) 60, 90 và 135.
Lời giải:
16 = 24 ; 24 = 23.3 ;
ƯCLN(16,24) = 23 = 8.
Các ước chung của 16 và 24 chính là các ước của 8. Đó là 1 ; 2 ; 4 và 8.
ƯCLN(180 , 234) = 18. Các ước chung là 1 , 2 , 3 , 6 , 9 , 18.
ƯCLN(60 , 90 , 135) = 15. Các ước chung là : 1 , 3 , 5 , 15.
2. Dạng 2: Tìm các ước chung của hai hay nhiều số thỏa mãn điều kiện cho trước
Bước 1. Tìm ƯCLN của hai hay nhiều số trước
Bước 2. Tìm các ước của ƯCLN này
Bước 3. Chọn trong số đó các ước thỏa mãn điều kiện đã cho
Bài 1: Tìm số tự nhiên a lớn nhất biết rằng 420 chia hết cho a và 700 chia hết cho a.
Lời giải
Theo đề bài a phải là ƯCLN của 420 và 700.
ƯCLN(420, 700) = 140.
Vậy a = 140.
Bài 2: Tìm các ước chung cua 24 và 180 thông qua tìm ƯCLN
Lời giải:
Phân tích các số ra thừa số nguyên tố
24 = 23 . 3
180 = 22 . 32 . 5
Từ đó Ư CLN (24; 180) = 22 . 3 = 12
Mà Ư (12) = {1; 2; 3; 4; 6; 12}
Vậy ƯC (24; 180) = {1; 2; 3; 4; 6; 12}
Bài 3: Tìm các ước chung lớn hơn 20 của 144 và 192.
Lời giải:
UCLN(144, 192) = 48.
Ước của 48 = {1; 2; 3; 4; 6; 8; 12; 24; 48}
Các ước của 48 lớn hơn 20 là 24 và 48.
Vậy các ước chung lớn hơn 20 của 144 và 192 là 24 và 48.
Bài 4: Tìm x N, biết 56 x,196 x và 5 x 25
Lời giải
vì 56:x, 196:x nên x ∈ Ư(56,196)
Ta có: 56 = 23.7, 196 = 22.72
ƯCLN(56;96) = 22.7 =28
Ư(56;96)= Ư(28) = 1;2;4;7;14;28
Vì 5 〈 x 〈 25 nên x ∈ 7;14
3. Dạng 3: Bài đưa về việc tìm ước chung lớn nhất của hai hay nhiều số thỏa mãn điều kiện cho trước
Bước 1: Phân tích đề bài, suy luận để đưa về việc tìm ƯCLN của hau hay nhiều số
Bước 2. Áp dụng quy tắc 3 bước để tìm ƯCLN đó
Bài 1: Tìm số tự nhiên a lớn nhất biết rằng 420 chia hết cho a và 700 chia hết cho a.
Lời giải
Theo đề bài a phải là ƯCLN của 420 và 700.
ƯCLN(420, 700) = 140.
Vậy a = 140.
Bài 2: Lan có một tấm bìa hình chữ nhật kích thước 75cm và 105cm. Lan muốn cắt tấm bìa thành
các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết, không còn thừa mảnh
nào. Tính độ dài lớn nhất của cạnh hình vuông (số đo cạnh của hình vuông nhỏ là một số tự
nhiên với đơn vị là xăng-ti-mét).
Lời giải:
Để tấm bìa được cắt hết thành các mảnh nhỏ hình vuông bằng nhau thì độ dài mỗi cạnh
của hình vuông phải là ước chung của 75 và 105. Do đó độ dài lớn nhất của cạnh hình vuông
(tính bằng cm) là ƯCLN (75,105), tức là 15 cm.
Bài 3: Một mảnh đất hình chữ nhật có chiều dài 120m, chiều rộng 36m. Người ta muốn trồng cây xung quanh vườn sao cho mỗi góc vườn có một cây và khoảng cách giữa hai cây liên tiếp bằng nhau. Hỏi số cây phải trồng ít nhất là bao nhiêu?
Lời giải:
Muốn số cây phải trồng ít nhất thì khoảng cách giữa hai cây trồng liên tiếp phải lớn nhất, ta gọi khoảng cách này là a mét () thì a phải là số lớn nhất sao cho và .
Vậy a = ƯCLN(120; 36)
Ta có 36 = 22.32; 120 = 23.3.5 nên a = 22.3 = 12
Vậy khoảng cách lớn nhất giữa hai cây trồng liên tiếp là 12 m
Chu vi của vườn là: (120 + 36).2 = 312 (m)
Tổng số cây ít nhất phải trồng là: 312 : 12 = 26 (cây)
Bài 4: Cô giáo chủ nhiệm muốn chia 24 quyển vở, 48 bút bi và 36 gói bánh thành một số phần thưởng như nhau để trao trong dịp sơ kết học lỳ. Hỏi có thể chia được nhiều nhất bao nhiêu phân thưởng? Khi đó mỗi phần thưởng có bao nhiêu quyền vở, bút bi và gói bánh?
Lời giải:
Gọi a là số phần thương để cô giáo chủ nhiệm trao trong dịp sơ kết học kì (a € N*; a < 24)
Để số phần thưởng là nhiều nhất thì a phải là số lớn nhất sao cho 24 chia hết cho a, 48 chia hết cho a, 36 chia hết cho a
Tức là a = ƯC LN (24; 48; 36)
Ta có: 24 = 23 . 3
48 = 24 . 3
36 = 22 . 32
ƯCLN (24; 48; 36) = 22 . 3 = 12 => a = 12
Vậy có thể chia được nhiều nhất thành 12 phần thưởng
Trong đó có 2 quyền vở, 4 bút bi và 3 gói bánh
Bài 5: Đào và Mai mỗi người mua một số bút chì màu, trong mỗi hộp đều có nhiều hơn hai bút và số bút ở mỗi hộp bằng nhau. Biết rằng Đào mua được 28 bút và Mai mua được 36 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?
Lời giải:
Gọi a là số bút chì màu trong mỗi hộp.
Ta phải có: 28 chia hết cho a và 36 chia hết cho a (a > 2)
Do đó, a € Ư CLN (28; 36) và a > 2
Ta tìm được Ư CLN (28; 36) = 4 => Ư CLN (28; 36) = {1; 2; 4}
mà a > 2 nên a = 4.
Vậy mỗi hộp có 4 bút.
Hy vọng với những kiến thức mà chúng tôi vừa trình bày có thế giúp các bạn hiểu thêm được về ước chung lớn nhất là gì và cách tìm ước chung lớn nhất một cách dễ dàng hơn, để áp dụng giải các bài toán liên quan đến ước chung lớn nhất.




