Trong bài viết dưới đây, Hyundai Smart Phone sẽ chia sẻ lý thuyết về trực tâm là gì, tính chất trực tâm của tam giác, cách tìm trực tâm tam giác và cách xác định trực tập của tam giác và các dạng bài tập có lời giải chi tiết nhất để các bạn cùng tham khảo
Trực tâm là gì?
Trực tâm là giao điểm 3 đường cao tương ứng với 3 đỉnh của một tam giác. Mỗi tam giác chỉ có 1 trực tâm duy nhất. Trực tâm có thể nằm trong hoặc ngoài miền của tam giác.
Đường cao trong tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao.
Ví dụ: Tam giác ABC có ba đường cao là AM, BN, CP. Gọi H là giao điểm của ba đường cao trên thì H là trực tâm của tam giác ABC.
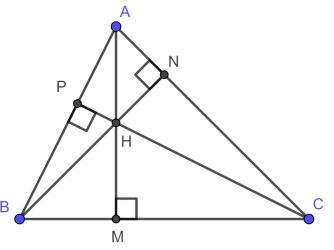
Tính chất của trực tâm trong tam giác
- Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đến trung điểm của một cạnh bằng ½ khoảng cách từ trực tâm tới đỉnh còn lại của tam giác đó.
- Trong tam giác cân, đường trung trực tương ứng với cạnh đáy đồng thời là đường phân giác, đường cao và đường trung tuyến của tam giác đó.
- Trong một tam giác, nếu đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
- Trong một tam giác, nếu đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác cân.
- Trực tâm của tam giác nhọn ABC trùng với tâm đường tròn nội tiếp tam giác được tạo bởi ba đỉnh là chân ba đường cao từ các đỉnh A, B, C đến các cạnh BC, AC, AB tương ứng.
- Đường cao tương ứng với một đỉnh của tam giác cắt đường tròn ngoại tiếp tam giác ở đâu thì điểm đó là điểm đối xứng với trực tâm của tam giác đó qua cạnh đáy đối xứng với đỉnh.
Hệ quả: Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.
Xem ngay: Công thức tính diện tích tam giác vuông, đều, cần kèm VD có lời giải
Cách xác định trực tâm của tam giác
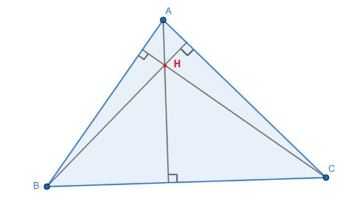
1. Trực tâm của tam giác nhọn
Trực tâm của tam giác nhọn nằm ở miền trong tam giác đó.
Ví dụ: Tam giác nhọn ABC có trực tâm H nằm ở miền trong tam giác.
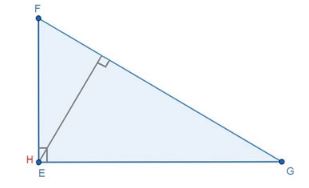
2. Trực tâm của tam giác vuông
Trực tâm chính là đỉnh góc vuông.
Ví dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông E.
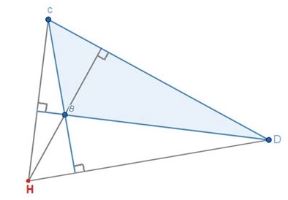
3. Trực tâm của tam giác tù
Trực tâm của tam giác tù nằm ở miền ngoài tam giác đó.
Ví dụ: Tam giác tù BCD có trực tâm H nằm ở miền ngoài tam giác
Tham khảo thêm: Hình chóp tam giác đều là gì? Tính chất, diện tích, thể tích hình chóp tam giác đều
Hướng dẫn cách vẽ trực tâm tam giác
Để vẽ trực tâm của một tam giác bạn cần thực hiện theo các bước sau:
- Bước 1: Vẽ tam giác bất kỳ.
- Bước 2: Tìm trung điểm của mỗi cạnh tam giác.
- Bước 3: Vẽ đường thẳng nối hai trung điểm của hai cạnh bất kỳ của tam giác.
- Bước 4: Lặp lại Bước 3 cho hai cặp trung điểm khác. Ba đường thẳng vừa được vẽ chính là ba đường trung tuyến của tam giác.
- Bước 5: Tìm giao điểm của ba đường trung tuyến. Điểm giao điểm này chính là trực tâm của tam giác.
Sau khi đã tìm được trực tâm, ta có thể dễ dàng vẽ được đường tròn nội tiếp và đường tròn ngoại tiếp của tam giác bằng cách lấy trực tâm làm tâm của đường tròn đó.
Cách tìm trực tâm của tam giác
Cho tam giác ABC có A (xa,ya), B(xb,yb), C(xc,yc) tìm tọa độ trực tâm H của tam giác ABC
Gọi AA’BB’lần lượt là hai đường cao xuất phát từ hai đỉnh A,B
Bước 1. Viết phương trình đường cao AA’
Giả sử phương trình đường cao ( AA’): A1x + B1y +C1 = 0
Bước 2. Viết phương trình đường cao BB’
Giả sử phương trình đường cao ( BB’): B2x + B2y +C2 = 0
Bước 3: Giải hệ hai phương trình bậc nhất hai ẩn
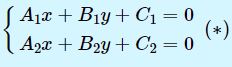
Giả sử nghiệm của (*) là (xh,yh)
Vậy tọa độ trực tâm H của tam giác ABC là (xh,yh)
Tham khảo thêm: Trọng tâm là gì? Tính chất, công thức tính trọng tâm tam giác
Bài tập về trực tâm của tam giác có lời giải chi tiết
Ví dụ 1: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.

Lời giải
Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
ΔHBC có :
AD ⊥ BC nên AD là đường cao từ H đến BC.
BA ⊥ HC tại F nên BA là đường cao từ B đến HC
CA ⊥ BH tại E nên CA là đường cao từ C đến HB.
AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.
Ví dụ 2: Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Lời giải
Xét ΔABC vuông tại A
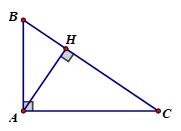
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
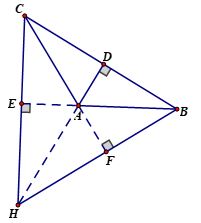
+ Giả sử E nằm giữa A và B, khi đó
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.
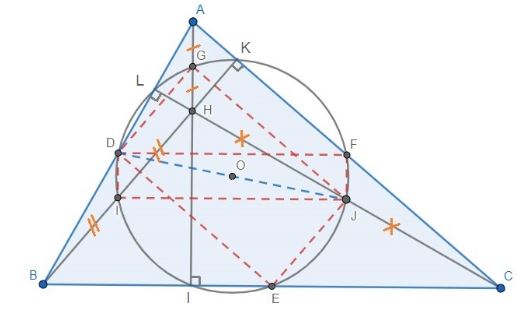
Ví dụ 3: Cho tam giác nhọn ABC với trực tâm H. Chứng minh rằng 9 điểm gồm chân ba đường cao; trung điểm ba cạnh và trung điểm các đoạn HA, HB, HC cùng nằm trên một đường tròn.
Lời giải
Gọi
- I, L, K lần lượt là chân ba đường cao hạ từ 3 đỉnh A, B và C. H là giao điểm ba đường cao.
- D, E, F lần lượt là trung điểm của 3 cạnh AB, BC và AC.
- G, I, J lần lượt là trung điểm của 3 đoạn AH, BH và CH.
Ta có:
DF là đường trung bình ▲ABC ⇒ DF//BC và DF = ½ BC. (1)
IJ là đường trung bình ▲HBC ⇒ IJ//BC và IJ = ½ BC. (2)
Từ (1) và (2) ⇒ DFJI là hình bình hành. (3)
Ta có: DI là đường trung bình ▲AHB ⇒ DI//AH nên DI//AI.
Mặc khác: AI ┴ BC và IJ//BC.
⇒ DI vuông góc với IJ. (4)
Từ (3) và (4) ta có DFJI là hình chữ nhật. Tâm đường tròn ngoại tiếp DFJI là O, O là trung điểm DJ. (a)
Tương tự chứng minh GDEJ là hình chữ nhật ngoại tiếp đường tròn tâm O, O là trung điểm DJ. (b)
GIE vuông tại I, suy ra tâm đường tròn ngoại tiếp ▲GIE là O trung điểm GE. Tương tự O cũng là tâm đường tròn ngoại tiếp ▲JLD và ▲IKF. (c)
Từ (a), (b) và (c) kết luận 9 điểm là chân đường cao, trung điểm các cạnh của ▲ABC và trung điểm 3 đoạn HA, HB, HC cùng nằm trên một đường tròn tâm O.
Ví dụ 4: Cho tam giác ABC có A(8,3), B(9,1), C(12,1) tìm tọa độ trực tâm H của tam giác ABC
Lời giải
Phương trình đường cao (AA’): x – 8 = 0
Phương trình đường cao (BB’): 2x – y – 17 = 0
Giả hệ hai phương trình bậc nhất hai ẩn

Vậy tọa độ trực tâm H của tam giác ABC là (8,-1)
Ví dụ 5:Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N. Chứng minh KN ⊥ IM.
Lời giải
Vẽ hình
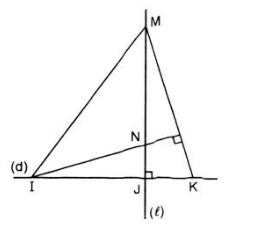
Trong một tam giác, ba đường cao đồng quy tại một điểm là trực tâm của tam giác đó.
l ⊥ d tại J, và M, J ∈ l ⇒ MJ ⟘ IK ⇒ MJ là đường cao của ΔMKI.
N nằm trên đường thẳng qua I và vuông góc với MK ⇒ IN ⟘ MK ⇒ IN là đường cao của ΔMKI.
IN và MJ cắt nhau tại N .
Theo tính chất ba đường cao của ta giác ⇒ N là trực tâm của ΔMKI.
⇒ KN cũng là đường cao của ΔMKI ⇒ KN ⟘ MI.
Vậy KN ⏊ IM
Ví dụ 6: Cho hình vẽ
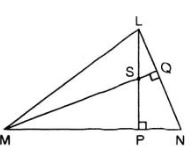
a) Chứng minh NS ⊥ LM
b) Khi góc LNP = 50o, hãy tính góc MSP và góc PSQ.
Lời giải
a) Trong ΔMNL có:
LP ⊥ MN nên LP là đường cao của ΔMNL.
MQ ⊥ NL nên MQ là đường cao của ΔMNL.
Mà LP, MQ cắt nhau tại điểm S
Nên: theo tính chất ba đường cao của một tam giác, S là trực tâm của tam giác.
⇒ đường thẳng SN là đường cao của ΔMNL.
hay SN ⊥ ML.
b)
+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :
ΔNMQ vuông tại Q có:

Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp bạn nhớ lại kiến thức trực tâm là gì, tính chất và cách xác định trực tâm của tam giác để áp dụng vào làm bài tập rồi nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi




