Bạn gặp bài toán yêu cầu tìm vectơ chỉ phương của đường thẳng nhưng bạn lại không biết cách làm như thế nào? Đừng lo lắng, Hyundai Smart Phone sẽ hướng dẫn cách tìm vectơ chỉ phương của đường thẳng kèm theo bài tập có lời giải minh họa chi tiết trong bài viết dưới đây
Vectơ chỉ phương là gì?
Vectơ u→ (u→ ≠ 0→) là vectơ chỉ phương của đường thẳng Δ nếu giá của vectơ u→ song song hoặc trùng với đường thẳng Δ.
Lưu ý:
- Nếu u→ = ( a; b) là vectơ chỉ phương của đường thẳng Δ thì vectơ ku→ (k≠0) cũng là vectơ chỉ phương của Δ
- Nếu đường thẳng Δ có vectơ pháp tuyến n→ = (a;b)thì đường thẳng đó có các vectơ chỉ phương là u→ = (b; −a), u’→ = (−b; a)
Cách tìm vectơ chỉ phương của đường thẳng
Cho đường thẳng Δ đi qua hai điểm A và B có: AB→ là vectơ chỉ phương của đường thẳng Δ
Cho u→ là vectơ chỉ phương của Δ ⇒ ku→ (k≠0) là vectơ chỉ phương của đường thẳng Δ

Cho đường thẳng Δ có vectơ pháp tuyến n→ = (a;b) thì đường thẳng đó có các vectơ chỉ phương là u→ = (b;−a), u’→ = (−b;a)
Cho đường thẳng d và d’. Biết d ⊥ d’: Nếu d’ có vectơ pháp tuyến n’→ = (a; b) thì vectơ chỉ phương của d là u→ = (a;b)
Cho đường thẳng d và d’. Biết d // d’ : Nếu d’ có vectơ pháp tuyến n’→= (a;b) thì vectơ chỉ phương của d là u→ =(−b;a), u→ = (b;−a)
Tham khảo thêm:
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số và bài tập có đáp án
- Lý thuyết về phương trình đường thẳng và các dạng bài tập có lời giải từ A – Z
- Tìm m để hàm số đồng biến, nghịch biến trên khoảng kèm VD
Bài tập tìm vectơ chỉ phương của đường thẳng có lời giải
Ví dụ 1: Cho đường thẳng d đi qua hai điểm A(1; 3) và B(4; 5). Xác định 3 vectơ chỉ phương của đường thẳng d.
Lời giải:
Do đường thẳng d đi qua hai điểm A(1; 3) và B(4; 5) nên ta có:
AB→ = (4 – 1; 5 – 3) = (3; 2) là một vectơ chỉ phương của đường thẳng d.
k.AB→ (k≠0) cũng là vectơ chỉ phương của đường thẳng d.
Chọn k = 2, ta có vectơ chỉ phương : u2→ = 2AB→ = 6;4)
Chọn k = 3, ta có vectơ chỉ phương: u3→ = 3AB→ = (9;6)
Ví dụ 2: Cho đường thẳng d có vectơ pháp tuyến là n→ = (1; 2). Tìm 2 vectơ chỉ phương của đường thẳng d.
Lời giải:
Đường thẳng d có vectơ pháp tuyến là n→ = (1; 2)
⇒ Vectơ chỉ phương u→ = (2; -1) và u→ = (−2;1)
Ví dụ 3: Cho hai đường thẳng d và d’. Tìm vectơ chỉ phương của d. Biết d ⊥ d’ và vectơ pháp tuyến của d’ là n’→ = (1;5).
Lời giải:
Do d ⊥ d’ và vectơ pháp tuyến của d’ là n’→ = (1;5)nên ta có:
Vectơ chỉ phương của d là u→ = (1;5)
Ví dụ 4: Cho đường thẳng d đi qua A(- 2; 3) và điểm B(2; m + 1) . Tìm m để đường thẳng d nhận u→ ( 2; 4) làm VTCP?
Lời giải
Đường thẳng d đi qua hai điểm A và B nên đường thẳng d nhận vecto AB→( 4; m – 2) làm VTCP.
Lại có vecto u→(2; 4) làm VTCP của đường thẳng d. Suy ra hai vecto u→ và ab→ cùng phương nên tồn tại số k sao cho: u→ = kAB
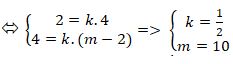
Vậy m = 10 là giá trị cần tìm
Ví dụ 5: Xác định vectơ chỉ phương của d: 2x – 3y + 2018 = 0
Lời giải
Đường thẳng d: 2x – 3y + 2018 = 0 có VTPT nd→ = (2; -3)nên ud→ = (3; 2) là một VTCP của d.
⇒ Vecto ( – 3; -2) cũng là VTCP của đường thẳng d.
Ví dụ 6: Đường thẳng d có một vectơ pháp tuyến là u→ = (-2; -5) . Đường thẳng ∆ vuông góc với d có một vectơ chỉ phương
Lời giải
Khi hai đường thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia nên:
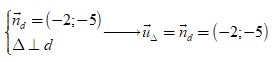
Lại có hai vecto u∆→( -2; -5) và u→( 2;5) cùng phương nên đường thẳng ∆ nhận vecto u→( 2; 5) làm VTCP.
Ví dụ 7: Đường thẳng d có một vectơ pháp tuyến là n→ = (-2; -5) . Đường thẳng song song với d có một vectơ chỉ phương
Lời giải
Khi hai đường thẳng song song với nhau thì VTCP ( VTPT) của đường thẳng này cũng là VTCP (VTPT) của đường thẳng kia nên:
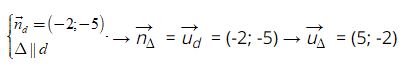
Bên trên chính là toàn bộ cách tìm vectơ chỉ phương của đường thẳng kèm theo bài tập mà chúng tôi vừa phân tích chi tiết có thể giúp các bạn áp dụng vào làm bài tập chính xác. Hãy thường xuyên theo dõi chúng tôi để được chia sẻ những kiến thức về vật lý, hóa học, toán học,…




