Lý thuyết về phương trình đường thẳng và các dạng bài tập có lời giải từ A – Z

Trong môn Toán bạn còn mơ hồ về phần phương trình đường thẳng thì hãy đọc ngay bài viết của Hyundai Smart Phone dưới đây sẽ được chia sẻ lý thuyết về phương trình đường thẳng trong mặt phẳng và trong không gian kèm theo các dạng bài tập thường gặp có lời giải chi tiết nhất

Phương trình đường thẳng trong mặt phẳng 

1. Phương trình tổng quát

Phương trình Δ : ax + by + c = 0 (a2 + b2 ≠ 0) là PTTQ của đường thẳng Δ nhận n^→ (a;b )làm vectơ pháp tuyến của đường thẳng

Trường hợp đặc biết:

• Nếu a = 0 ⇒y = −cb; Δ // Ox hoặc trùng Ox (khi c=0)
• Nếu b = 0 ⇒ x = −ca; Δ//Oy hoặc trùng Oy (khi c=0)
• Nếu c = 0 ⇒ ax + by = 0 ⇒ Δ đi qua gốc tọa độ

2. Phương trình đường thẳng theo đoạn chắn

Cho đường thẳng d cắt trục Ox và Oy lần lượt tại hai điểm A(a; 0) và B(0; b) với a≠0,b≠0, phương trình đường thẳng d theo đoạn chắn là: x⁄a + y/b = 1

3. Phương trình tham số của đường thẳng

Trong mặt phẳng Oxy cho đường thẳng d đi qua điểm M₀ (x₀; y₀)và có vectơ chỉ phương là u^→ = (a;b). Phương trình đường tham số của đường thẳng d là

t ∈ R.

4. Phương trình chính tắc của đường thẳng

Phương trình chính tắc của đường thẳng Δ đi qua M₀(x₀, y₀) và có vecto chỉ phương u^→ = (u₁, u₂) là

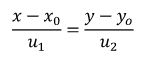
Với u₁, u₂ ≠ 0, (trường hợp ab = 0 thì đường thẳng không có phương trình chính tắc)

Lưu ý:

• Nếu hai đường thẳng song song với nhau thì chúng có cùng VTCP và VTPT.
• Hai đường thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại
• Nếu ∆ có VTCP u^→ = (a; b) thì n^→ = (-b; a) là một VTPT của ∆

Xem ngay: Ma trận nghịch đảo là gì? Cách tìm ma trận nghịch đảo 2×2, 3×3, 4×4

5. Vị trí tương đối của hai đường thẳng

Xét hai đường thẳng ∆₁ và ∆₂ có phương trình tổng quát lần lượt là : a₁x+b₁y + c₁ = 0 và a₂x+b₂y +c₂ = 0

Điểm M₀ (x₀;y₀) là điểm chung của ∆₁ và ∆₂ khi và chỉ khi (x₀;y₀) là nghiệm của hệ hai phương trình:

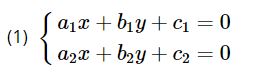
Ta có các trường hợp sau:

• Hệ (1) có một nghiệm: ∆₁ cắt ∆₂
• Hệ (1) vô nghiệm: ∆₁ // ∆₂
• Hệ (1) có vô số nghiệm: ∆₁ ≡ ∆₂

6. Vị trí tương đối của đường thẳng với mặt phẳng

Cho đường thẳng d đi qua M0 (x₀,y₀,z₀ ) và có vectơ chỉ phương u^→ = (a,b,c) và mặt phẳng (P): Ax + By + Cz + D = 0 có vecto pháp tuyến u^→ = (A,B,C). Khi đó

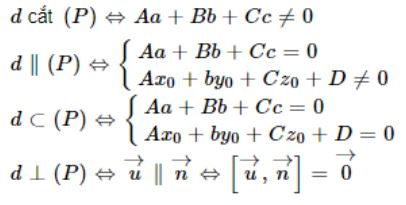
7. Góc giữa hai đường thẳng

Cho hai đường thẳng d và d’ có vectơ chỉ phương lần lượt là: u^→ = (a;b) và u’^→= (a’;b’). Góc giữa hai đường thẳng được xác định bởi:

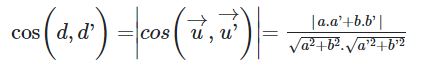
Cho hai đường thẳng d và d’ có vectơ pháp tuyến lần lượt là: n^→ = (a;b) và n’^→=(a’;b’). Góc giữa hai đường thẳng được xác định bởi:

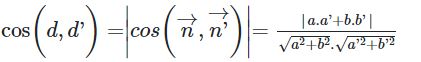
Gọi k và k’ lần lượt là hệ số góc của hai đường thẳng d và d’. Ta có:

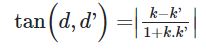
Tham khảo thêm: Lý thuyết và cách xác định góc giữa hai mặt phẳng kèm theo bài tập có lời giải

8. Khoảng cách từ một điểm đến đường thẳng

Cho đường thẳng d: ax + by + c = 0 và điểm M ( x₀; y₀). Khi đó khoảng cách từ điểm M đến đường thẳng d là

Cho điểm A( x_A; y_A) và điểm B( x_B; y_B) . Khoảng cách hai điểm này là : AB = √(x_B – X_A)² + (y_B -Y_A)²

Lưu ý: Trong trường hợp đường thẳng d chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng d về dạng tổng quát.

9. Khoảng cách giữa 2 đường thẳng chéo nhau

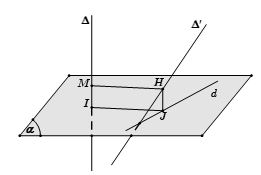
Dựng đoạn vuông góc chung MN của a và b, khi đó d (a,b) = MN. Tuy nhiên, khi dựng đoạn vuông góc chung MN, chúng ta có thể sẽ gặp phải các trường hợp sau:

Trường hợp 1: ∆ và ∆’ vừa chéo vừa vuông góc với nhau

Khi gặp trường hợp này, chúng ta sẽ làm như sau:

• Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I
• Bước 2: Trong mặt phẳng (α) kẻ đường thẳng IJ vuông góc với ∆’

Khi đó IJ chính là đoạn vuông góc chung và d (∆, ∆’) = IJ.

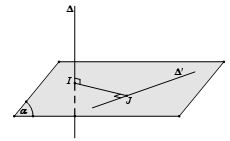
Trường hợp 2: ∆ và ∆’ chéo nhau mà không vuông góc với nhau

• Bước 1: Bạn chọn một mặt phẳng (α) chứa ∆’ và song song với ∆
• Bước 2: Bạn dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm M thuộc ∆ dựng đoạn MN vuông góc với (α) . Khi đó, d sẽ là đường thẳng đi qua N và song song với ∆
• Bước 3: Bạn gọi H là giao điểm của đường thẳng d với ∆’, dựng HK // MN

Khi đó, HK chính là đoạn vuông góc chung và d (∆, ∆’) = HK = MN.

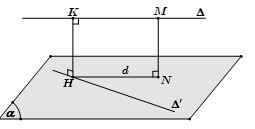
Hoặc bạn làm như sau:

• Bước 1: Chọn mặt phẳng (α) vuông góc với ∆ tại I
• Bước 2: Bạn tìm hình chiếu d của ∆’ xuống mặt phẳng (α)
• Bước 3: Trong mặt phẳng (α), dựng IJ vuông góc với d, từ J bạn dựng đường thẳng song song với ∆ và cắt ∆’ tại H, từ H dựng HM // IJ

Khi đó, HM chính là đoạn vuông góc chung và d (∆, ∆’) = HM = IJ.

Phương trình đường thẳng trong không gian

1. Phương trình tham số của đường thẳng

Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm M₀ (x₀ ; y₀; z₀) và nhận vectơ a = (a₁;a₂;a₃) làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M(x; y; z) nằm trên đường thẳng ∆ là có số thực t thỏa mãn:

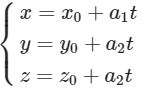
Phương trình tham số của đường thẳng ∆ đi qua điểm M₀ (x₀ ; y₀; z₀) và nhận vectơ a^→ = (a₁;a₂;a₃)làm vectơ chỉ phương là

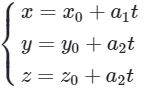
Trong đó, t là tham số.

2. Phương trình chính tắc

Nếu a₁ ; a₂; a₃ đều khác 0 thì ta có thể viết phương trình ∆ dưới dạng chính tắc như sau: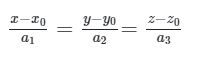

Xem ngay: Tập xác định của hàm số mũ, lũy thừa, logarit kèm VD có lời giải

Các dạng bài tập về phương trình đường thẳng có lời giải

1. Dạng 1: Cách viết các dạng phương trình đường thẳng.

Phương pháp giải:

a) Cách viết phương trình tổng quát của đường thẳng Δ

+ Tìm vectơ pháp tuyến n^→ (a; b) của đường thẳng Δ

+ Tìm một điểm M(x₀;y₀) thuộc Δ

+ Viết phương trình theo công thức: a(x-x₀) + b(y-y₀) = 0

+ Biến đổi thành dạng ax + by + c = 0

Nếu đường thẳng Δ₁ song song với đường thẳng Δ₂: ax + by + c = 0 thì Δ₁ có phương trình tổng quát ax + by + c’ = 0, c ≠ c’.

Nếu đường thẳng Δ₁ vuông góc với đường thẳng Δ₂ : ax + by + c = 0 thì có phương trình tổng quát -bx + ay + c’ = 0, c ≠ c’.

b) Cách viết phương trình tham số của đường thẳng

+ Tìm vectơ chỉ phương u^→ = (u₁;u₂) của đường thẳng Δ

+ Tìm một điểm M(x₀;y₀) thuộc Δ

Nếu Δ có hệ số góc k thì Δ có vectơ chỉ phương u^→ = (1;k)

Nếu Δ có vectơ pháp tuyến n^→ (a;b) thì Δ có vectơ chỉ phương u^→ = (-b;a) hoặc u^→ = (b;-a) và ngược lại.

c) Cách viết phương trình chính tắc của đường thẳng Δ . (chỉ áp dụng khi có vectơ chỉ phương u^→ = (a;b) với a.b#0)

+ Tìm vectơ chỉ phương u^→ = (a;b) (a.b#0) của đường thẳng Δ

+ Tìm một điểm M(x₀;y₀) thuộc Δ

d) Cách viết phương trình đoạn chắn của đường thẳng Δ (chỉ áp dụng khi đường thẳng cắt hai trục Ox, Oy)

+ Tìm hai giao điểm của Δ với trục Ox, Oy lần lượt là A(a; 0), B(0; b)

+ Viết phương trình đoạn chắn x/a + y/b = 1 (a.b ≠0)

Ví dụ 1: Cho đường thẳng d cắt trục Ox, Oy tại hai điểm A(0; 5) và B(6; 0). Viết phương trình tổng quát và phương trình đoạn chắn của đường thẳng d.

Lời giải:

Vì A(0; 5) và B(6; 0) thuộc đường thẳng d nên ta có AB^→ là vectơ chỉ phương của đường thẳng d.

AB^→ = (6-0;0-5) = (6;-5)

⇒ Vectơ pháp tuyến của d là n^→ (5;6)

Chọn điểm A(0; 5) thuộc đường thẳng d, ta có phương trình tổng quát của đường thẳng d:

5.(x – 0) + 6.(y – 5) = 0

Phương trình đường thẳng và cách giải bài tập hay, chi tiết 5x + 6y – 30 = 0

Vì đường thẳng d cắt trục Ox, Oy lần lượt tại hai điểm A(0; 5) và B(6; 0) nên ta có phương trình đoạn chắn là:

x/6 + y/5 =1

Ví dụ 2: Cho đường thẳng d đi qua hai điểm M(5; 8) và N(3; 1). Viết phương trình tham số và phương trình chính tắc của đường thẳng d.

Lời giải:

Vì M(5; 8) và N(3; 1) thuộc đường thẳng d nên ta có MN^→ là vectơ chỉ phương của đường thẳng d, có:

MN^→= (3 – 5; 1 – 8) = (-2; -7)

Chọn điểm N(3; 1) thuộc đường thẳng d ta có phương trình tham số của đường thẳng d:

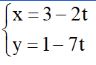
Chọn điểm M(5; 8) thuộc đường thẳng d ta có phương trình chính tắc của đường thẳng d:

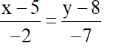
2. Dạng 2: Vị trí tương đối giữa hai đường thẳng.

Phương pháp giải: Áp dụng lí thuyết về vị trí tương đối giữa hai đường thẳng: d₁: a₁x + b₁y + c₁ = 0 và d₂: a₂x + b₂y + c₂ = 0 với a₁₂ + b₁₂# 0, a₂₂ + b₂₂ #0.

Tọa độ giao điểm của hai đường thẳng đó là nghiệm của hệ phương trình:

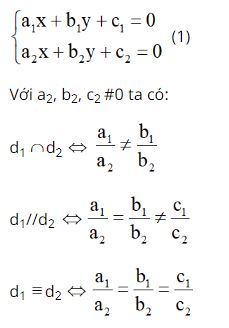
Ví dụ: Xét vị trí tương đối của hai đường thẳng sau:

a) d₁: 4x – 10y + 1 = 0 và d₂ : x + y + 2 = 0.

b) d₃: 12x – 6y + 10 = 0 và d₄ : 2x – y + 5 = 0.

c) d₅: 8x + 10y – 12 = 0 và d₆ : 4x + 5y – 6 = 0.

Lời giải

3. Dạng 3: Tính góc giữa hai đường thẳng.

Phương pháp giải: Áp dụng lí thuyết về góc giữa hai đường thẳng:

Cho hai đường thẳng d₁: a₁x + b₁y + c₁ = 0 có vectơ pháp tuyến n₁^→ và d₂: a₂x + b₂y + c₂ = 0 có vectơ pháp tuyến n₂^→ với a₁₂ + b₁₂ # 0, a₂₂ + b₂₂ #0, góc giữa hai đường thẳng được kí hiệu là (d₁,d₂), (d₁,d₂) luôn nhỏ hơn hoặc bằng 90⁰ Đặt α = (d₁,d₂) ta có:

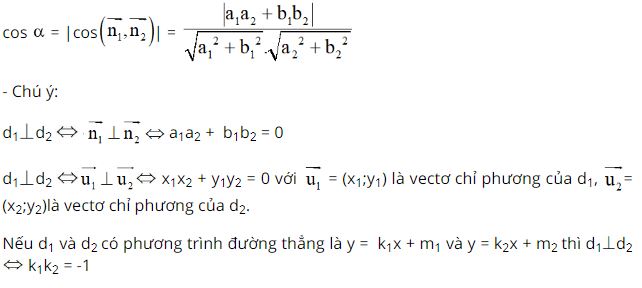
Ví dụ: Cho hai đường thẳng d: 4x – 2y + 6 = 0 và d’: x + 2y + 1 = 0. Xác định số đo góc giữa d và d’.

Lời giải:

Xét d: 4x – 2y + 6 = 0 ta có vectơ pháp tuyến của d là n^→ = (4; -2)

Xét d’: x + 2y + 1 = 0 ta có vectơ pháp tuyến của d’ là n’^→ = (1; 2)

Ta có: n^→ .n’^→= 4.1 + (-2).2 = 0

⇒ d ⊥ d’

⇒ (d;d’) = 90 ⁰

4. Dạng 4: Khoảng cách từ một điểm đến một đường thẳng.

Phương pháp giải: Áp dụng lí thuyết về khoảng cách từ một điểm đến một đường thẳng: Trong mặt phẳng Oxy, đường thẳng Δ có phương trình ax + by + c = 0 và điểm M(x0;y0) . Khoảng cách từ điểm M đến đường thẳng Δ được kí hiệu là d (M,Δ ), tính bằng công thức:

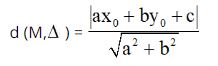
Ví dụ: Cho điểm A (3; 6). Tìm khoảng cách từ A đến đường thẳng d:

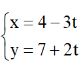
Lời giải

Xét đường thẳng d: 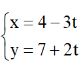ta có vectơ chỉ phương của d là u^→ = (-3; 2)

vectơ pháp tuyến của d là n^→ = (2; 3)

Chọn điểm M (4; 7) thuộc d ta có phương trình tổng quát của d là:

2.(x – 4) + 3.(y – 7) = 0

⇔ 2x – 8 + 3y – 21 = 0

⇔ 2x + 3y – 29 = 0

Khoảng cách từ A (3; 6) đến đường thẳng d là:

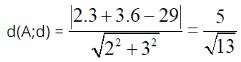
Bên trên chính là toàn bộ lý thuyết về phương trình đường thẳng trong mặt phẳng, không gian mà chúng tôi vừa phân tích chi tiết có thể giúp các bạn củng cố lại kiến thức để áp dụng vào làm bài tập nhé.