Nếu các bạn muốn biết tìm hiểu lý thuyết góc giữa hai mặt phẳng là gì và cách xác định góc giữa hai mặt phẳng hoặc công thức tính góc giữa hai mặt phẳng thì hãy đọc ngay bài viết dưới đây của Hyundai Smart Phone sẽ được cũng cố lại kiến thức hình học đồng thời chia sẻ các dạng bài tập tính góc giữa hai mặt phẳng trong không gian. Nào chúng ta cùng nhau bắt đầu nhé
Góc giữa hai mặt phẳng là gì?
Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Trong không gian 3 chiều, góc giữa 2 mặt phẳng còn được gọi là góc khối là phần không gian bị giới hạn bởi 2 mặt phẳng.
Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng.
Tính chất của góc giữa 2 mặt phẳng
- Góc giữa 2 mặt phẳng song song bằng 0 độ,
- Góc giữa 2 mặt phẳng trùng nhau bằng 0 độ.
Tham khảo thêm: Hình thang vuông là gì? Tính chất, Công thức tính chu vi, diện tích hình thang vuông
Cách xác định góc giữa 2 mặt phẳng
Gọi P là mặt phẳng 1, Q là mặt phẳng 2
Trường hợp 1: Hai mặt phẳng (P), (Q) song song hoặc trùng nhau thì góc của 2 mặt phẳng bằng 0,
Trường hợp 2: Hai mặt phẳng (P), (Q) không song song hoặc trùng nhau.
Cách 1: Dựng 2 đường thẳng n và p vuông góc lần lượt với 2 mặt phẳng (P), (Q). Khi đó góc giữa 2 mặt phẳng (P), (Q) là góc giữa 2 đường thẳng n và p.
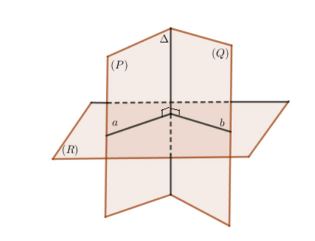
Cách 2: Để xác định góc giữa 2 mặt phẳng đầu tiên bạn cần xác định giao tuyến Δ của 2 mặt phẳng (P) và (Q). Tiếp theo, bạn tìm một mặt phẳng (R) vuông góc với giao tuyến Δ của 2 mặt phẳng (P), (Q) và cắt 2 mặt phẳng tại các giao tuyến a, b.
⇒ Góc giữa 2 mặt phẳng (P), (Q) là góc giữa a và b.
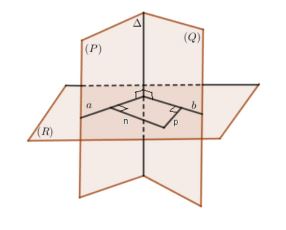
Cách 3: Sử dụng công thức hình chiếu: Gọi S là diện tích của hình (H) trong mp(α) và S’ là diện tích hình chiếu (H’) của (H) trên mp(β) thì S’ = S.cosφ
⇒ cosα ⇒ φ
Công thức tính góc giữa hai mặt phẳng
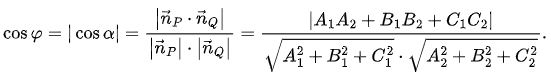
Tham khảo thêm: Tích Có Hướng, Tích Vô Hướng của 2 Vecto là gì? Định nghĩa, tính chất, ứng dụng
Phương pháp tính góc giữa 2 mặt phẳng
Có 2 phương pháp bạn có thể áp dụng để tính góc giữa 2 mặt phẳng:
Phương pháp 1: Sử dụng hệ thức lượng trong tam giác vuông, định lý hàm số sin, hàm số cos.
Ví dụ 1: Cho hình chóp tứ giác đều S.ABCD có đáy là ABCD và độ dài các cạnh đáy bằng a, SA = SB = SC = SD = a. Tính cos góc giữa hai mặt phẳng (SAB) và (SAD).
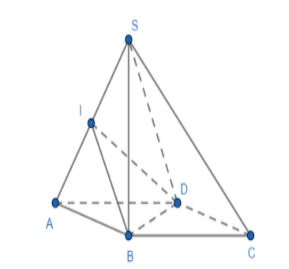
Lời giải
Gọi I là trung điểm đoạn SA. Ta có tam giác SAD và tam giác SAB đều
Suy ra BI ⊥ SA, DI ⊥ SA
⇒ ![]()
Áp dụng định lý cosin vào tam giác BID ta được:
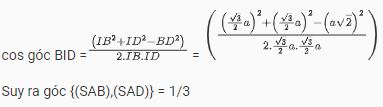
Phương pháp 2: Dựng mặt phẳng phụ (R) vuông góc với giao tuyến c mà (Q) giao với (R) = a, (P) giao với (R) = b. Suy ra (Â) = (Q∧) = (a∧,b)
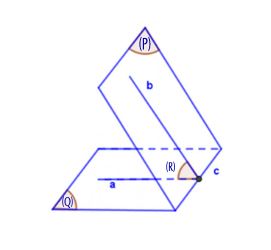
Ví dụ: Cho hình chóp S.ABCD, cạnh đáy ABCD là nửa lục giác đều nội tiếp đường tròn có đường kính AB = 2a, SA vuông góc với mặt phẳng (ABCD) và SA = a√3. Tính góc giữa hai mặt phẳng (SBC) và (SCD).
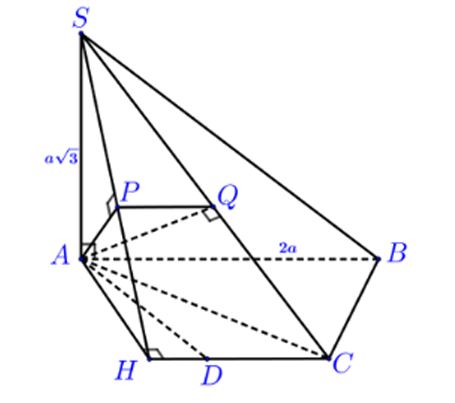
Lời giải:
Theo đề bài ta có ABCD là nửa lục giác đều nên AD = DC = CB = a
Dựng đường thẳng đi qua điểm A vuông góc với mặt phẳng (SCD)
Trong mặt phẳng (ABCD) dựng AH vuông góc với CD tại H ⇒ ta có CD vuông góc với mặt phẳng (SAH).
Trong mặt phẳng (SAH) dựng AP vuông góc với SH ⇒ ta có CD vuông góc với AP ⇒ AP vuông góc với mặt phẳng (SCD).
Tiếp theo, dựng đường thẳng đi qua A vuông góc với mặt phẳng (SBC)
Trong mặt phẳng (SAC) dựng đường AQ vuông góc với SC,
Vì BC vuông góc với AC, BC vuông góc với SA => BC vuông góc với mặt phẳng (SAC) ⇒ BC vuông góc với AQ.
Vậy AQ vuông góc với mặt phẳng (SBC).
⇒ Góc giữa 2 mặt phẳng (SBC) và (SCD) chính là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng ấy là AP và AQ.
Ta có :
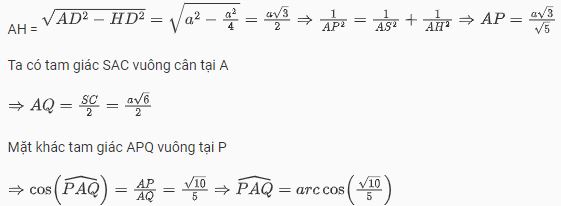
Các dạng bài tập tính góc giữa hai mặt phẳng trong không gian có lời giải
Ví dụ 1: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là ∠CBD
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB
C. (BCD) ⊥ (AIB)
D. (ACD) ⊥ (AIB)
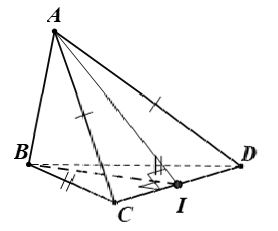
Lời giải
Tam giác BCD cân tại B có I trung điểm đáy CD
⇒ CD ⊥ BI (1)
Tam giác CAD cân tại A cóI trung điểm đáy CD
⇒ CD ⊥ AI (2)
Từ (1) và (2) ⇒ CD ⊥ (ABI).
⇒ (BCD) ⊥ (ABI) Và (ACD) ⊥ (ABI);
Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB .
Vậy A: sai ⇒Chọn A
Ví dụ 2: Cho hình chóp S.ABC với đáy ABC là tâm giác vuông cân tại điểm B. SA = a và vuông góc với (ABC). Cho AB =BC = a. Yêu cầu: Tính góc giữa hai mặt phẳng (SAC) và (SBC).
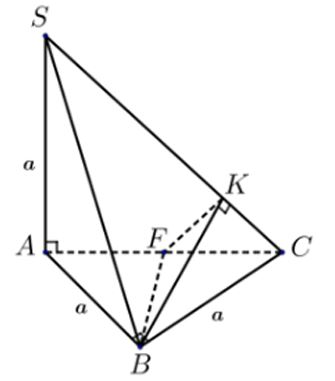
Lời giải
Theo đề bài ta có (SAC) giao với (SBC) = SC,
Gọi F là trung điểm đoạn AC. Suy ra BF vuông góc với mặt phẳng (SAC).
Dựng BK vuông góc với SC tại K
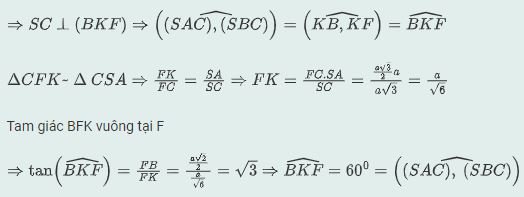
Ví dụ 3: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy
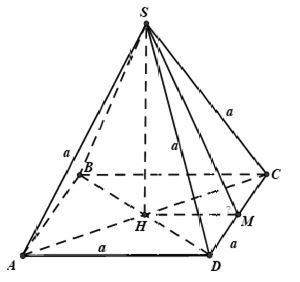
Lời giải:
Gọi H là giao điểm của AC và BD.
Do S.ABCD là hình chóp tứ giác đều nên SH ⊥( ABCD)
Ta có: (SCD) ∩ (ABCD) = CD. Gọi M là trung điểm CD.
Tam giác SCD là cân tại S ; tam giác CHD cân tại H (Tính chất đường chéo hình vuông)
SM ⊥ CD và HM ⊥ CD
⇒ ((SCD), (ABCD)) = (SM, HM) = ∠SMH = α
Từ giả thiết suy ra tam giác SCD là tam giác đều cạnh a có SM là đường trung tuyến ⇒ SM = a√3/2
⇒ 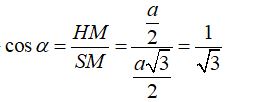
Ví dụ 4: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF)và (SBC) là bao nhiêu?
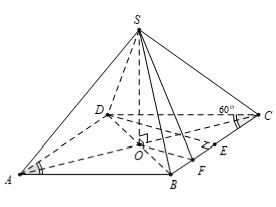
Lời giải
Tam giác BCD có BC = BD và ∠BCD = 60° nên tam giác BCD đều
Lại có E là trung điểm BC ⇒ DE ⊥ BC
Mặt khác, tam giác BDE có OF là đường trung bình
⇒ OF // DE ⇒ BC ⊥ OF (1).
Do SO ⊥ (ABCD) ⇒ BC ⊥ SO (2).
Từ (1) và (2), suy ra BC ⊥ (SOF) ⇒ (SBC) ⊥ (sOF)
Vậy, góc giữa ( SOF) và( SBC) bằng 90°
Ví dụ 5: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a; AD = 2a. Gọi α là góc giữa đường chéo A’C và đáy ABCD. Tính α .
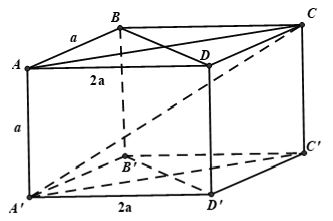
Lời giải
Từ giả thiết ta suy ra: AA’ ⊥ (ABCD) nên AC là hình chiếu vuông góc của A’C lên mặt phẳng (ABCD)
⇒ (A’C, (ABCD)) = (A’C, AC) = ∠A’CA = α
Áp dụng định lý Pytago trong tam giác ABC vuông tại B ta có:
AC2 = AB2 + BC2 = a2 + 4a2 = 5a2 ⇒ AC = a√5 .
Áp dụng hệ thức lượng trong tam giác AA’C vuông tại A ta có:
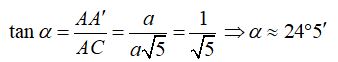
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD); SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60°.
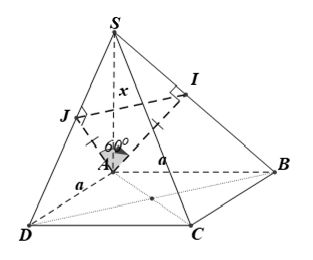
Lời giải
Trong (SAB) dựng AI ⊥ SB ta chứng minh được AI ⊥ (SBC) (1)
Trong (SAD) dựng AJ ⊥ SD ta chứng minh được AJ ⊥ (SCD) (2)
Từ (1) và (2) ⇒ góc ((SBC), (SCD)) = (AI, AJ) = ∠IAJ
Ta chứng minh được AI = AJ. Do đó, nếu góc ∠IAJ = 60° thì ΔAIJ đều ⇒ AI = AJ = IJ
Tam giác SAB vuông tại A có AI là đường cao
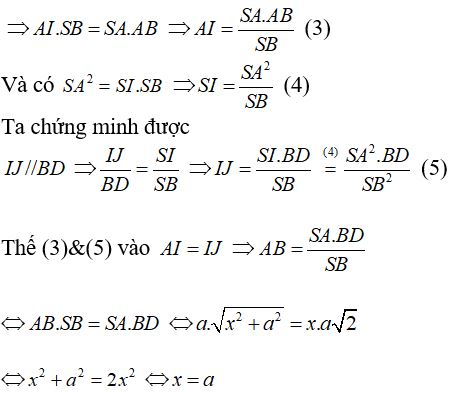
Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn củng cố lại kiến thức về cách xác định góc giữa hai mặt phẳng để áp dụng vào làm bài tập rồi nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi




