Nếu bạn muốn biết công thức tính diện tích hình quạt tròn cũng như chu vi hình quạt tròn thì hãy đọc ngay bài viết dưới đây của Hyundai Smart Phone sẽ được giải đáp chi tiết kèm theo các dạng bài tập có lời giải minh họa giúp bạn củng cố lại kiến thức.
Hình quạt tròn là gì?
Trong hình học phẳng, hình quạt tròn là phần của hình tròn được giới hạn bởi hai bán kính và cung tròn chắn bởi hai bán kính này.
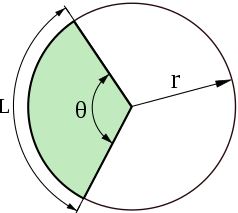
Công thức tính diện tích hình quạt tròn
S = πR 2 n/360 hay S = lR/2
Trong đó:
- S là diện tích của hình quạt tròn;
- R là bán kính đường tròn
- l là độ dài cung n0 của hình quạt tròn
Công thức tính chu vi hình quạt tròn
C = 2R + l
Trong đó:
- C là chu vi hình tròn quạt
- R là bán kính của đường tròn tâm O
- l là chiều dài cung
Tham khảo thêm: Hình vuông là gì? Tính chất, chu vi và diện tích hình vuông kèm VD
Bài tập áo dụng công thức tính chu vi, diện tích hình quạt tròn có đáp án
Ví dụ 1: Tính chu vi hình quạt tròn có:
a) bán kính R = 4 cm, chiều dài cung ℓ = 8 cm.
b) bán kính R = 2 mm, chiều dài cung ℓ = 1 cm.
c) bán kính R = 3 cm, chiều dài cung ℓ = 30 mm.
Lời giải
a) Ta có: R = 4 cm, ℓ = 8 cm
Áp dụng công thức tính chu vi hình quạt tròn:
C = 2R + ℓ = 2,4 + 8 = 16 cm.
b) Ta có: R = 2 mm = 0,2 cm, ℓ = 1 cm
Áp dụng Công thức tính chu vi của hình quạt tròn là
C = 2R + ℓ = 2,0,2 + 1 = 1,4 cm
c) Ta có: R = 3 cm, ℓ = 30 mm = 3 cm
Áp dụng công thức tính chu vi của quạt tròn:
C = 2R + ℓ = 2,3 + 3 = 9 cm
Ví dụ 2: Hãy tính chu vi của một hình quạt có diện tích 8 cm2, cung có độ dài 5 cm.
Lời giải
Ta có:
S = l.R/2 ⇒ R = 2S/l = 2,8 : 5 = 3,2 cm
Dựa theo công thức tính chu vi hình quạt ta có: C = 2R + ℓ = 2.3,2 + 5 = 11,4 (cm).
Ví dụ 3: Cho đường tròn (O; 8cm) đường kính AB. Điểm M ∈ (O) sao cho góc BAM = 600. Tính diện tích hình quạt AOM
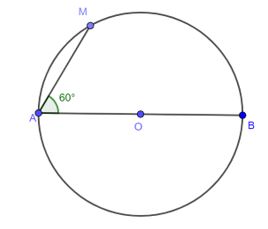
Lời giải:
Xét đường tròn (O) có:
BAM = 600
Suy ra số do cung nhỏ BM bằng
2.600 = 1200
Do đó số do cung nhỏ AM bằng:
n0 = 1800 – 1200 = 600
Vậy diện tích hình quạt AOM là
S = πR 2 n/360 = (π.8 2 .60) : 360 = 32π/3 (cm 2 )
Ví dụ 3: Cho đường tròn (O; R) và một điểm M sao cho OM = 2R. Từ M vẽ các tiếp tuyến MA và MB với A, B là các tiếp điểm.
a) Tính độ dài cung nhỏ AB.
b) Tính diện tích giới hạn bởi hai tiếp tuyến AM; BM và cung nhỏ AB.

Lời giải
a) Vì AM là tiếp tuyến của đường tròn (O) nên AM vuông góc với OA.
Xét tam giác OAM vuông tại A ta có:
cos AOM∧ = OA/OM = R⁄2R = 1⁄2 (tỉ số lượng giác trong tam giác vuông)
⇒ AOM∧ = 600. Mà OM là tia phân giác của góc AOB∧ (tính chất hai tiếp tuyến cắt nhau)
⇒ AOB∧ = 1200
b) Xét tam giác OAM vuông tại A ta có:
AM2 + AO2 = OM2 (định lý Pytago)
⇔ AM 2 + R 2 = (2R) 2
⇔ AM 2 = 4R 2 – R 2
⇔ AM = √3R (đơn vị độ dài)
Diện tích tam giác OAM là:
S = ½AM.AO = ½.R.√3R = √3R2/2 (đơn vị diện tích)
Xét tam giác AOM và tam giác BOM có:
OM chung
AO = BO = R
AM = BM (tính chất hai tiếp tuyến cắt nhau)
Do đó ΔAOM = ΔBOM (c.c.c)
⇒ S AOM = S BOM = √3R 2 /2

Ví dụ 4: Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB, vẽ dây tại M. Giả sử AM = 2 cm và CD =
4√3cm. Tính
a) Độ dài đường tròn (O) và diện tích hình tròn.
b) Độ dài cung CAD và diện tích hình quạt tròn giới hạn bởi hai bán kính OC, OD và cung nhỏ CD.
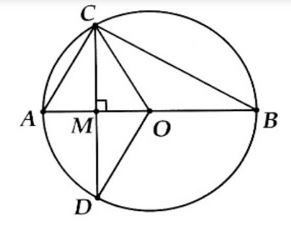
Lời giải
Một)
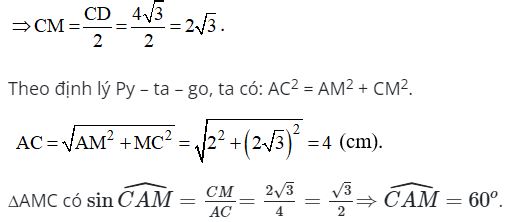
∆OAC cân tại O (vì OA = OC) có góc CAO = 60 nên ∆OAC đều
Suy ra OA = AC = 4 (cm).
Độ dài đường tròn (O) là: C = 2πR = 8π (cm).
Diện tích hình tròn (O) là: S = πR2 = 16π (cm2).
b) ∆OAC đều suy tra góc AOC = 600
∆OCD cân tại O có OM là đường cao nên OM cũng là đường phân giác hay

Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nhớ được định nghĩa hình quạt tròn là gì, công thức tính diện tích hình quạt tròn và chu vi hình quạt tròn để áp dụng vào làm bài tập rồi nhé. Hãy thường xuyên theo dõi chúng tôi để được chia sẻ kinh nghiệm bổ ích khác.




