Ở phần hình học hôm nay, Hyundai Smart Phone tiếp tục chia sẻ tới các bạn đọc công thức tính thể tích khối cầu, diện tích mặt cầu và các bài tập minh họa có đáp án chi tiết trong bài viết dưới đây để các bạn cùng tham khảo nhé.
Khối cầu là gì?
Khối cầu là tập hợp những điểm nằm trong mặt cầu và mặt cầu được gọi là hình cầu hay khối cầu có tâm O bán kính là R = OA.
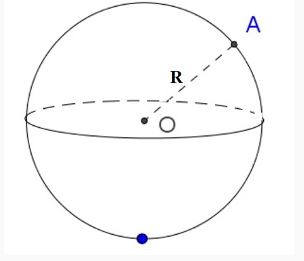
Công thức tính diện tích mặt cầu
Diện tích mặt cầu bằng bốn lần hằng số Pi nhân với bình phương bán kính của hình cầu. Hoặc diện tích mặt cầu bằng số pi nhân với bình phương đường kính của hình cầu
S = 4πr2 = πd2
Trong đó:
- S là diện tích mặt cầu
- r là bán kính khối cầu
- d là đường kính khối cầu
- π là hằng số có giá trị bằng 3,14
Xem ngay: Hình hộp chữ nhật là gì? Tính chất, diện tích, thể tích hình hộp chữ nhật kèm VD
Công thức tính thể tích khối cầu
Thể tích khối cầu (hình cầu) được tính bằng 3⁄4 của Pi nhân với lập phương bán kính hình cầu hoặc bằng 1⁄6 của Pi nhân với lập phương đường kính hình cầu
V = 3⁄4π.r3 = 1⁄6π.d3
Trong đó:
- V là thể tích mặt cầu
- r là bán kính khối cầu
- d là đường kính khối cầu
- π là hằng số có giá trị bằng 3,14
Tham khảo thêm: Thể tích khối nón là gì? Công thức tính khối nón tròn xoay, khối nón cụt
Bài tập áp dụng công thức tính thể tích khối cầu, diện tích mặt cầu có lời giải
Ví dụ 1: Một hình cầu có thể tích bằng 972π cm3. Tính diện tích của mặt cầu đó.
Lời giải
Bán kính của mặt cầu đó là:
3⁄4π.r3 = 972π ⇔ r3 = 972
⇒ r= 9 cm
Diện tích của mặt cầu đó là:
S = 4πR2 = 4π . 92 = 324π (cm2)
Vậy diện tích của mặt cầu đó là 324π cm2.
Ví dụ 2: Hai hình cầu có hiệu các bán kính bằng 3 cm và hiệu các thể tích bằng 1332π cm3. Tính hiệu các diện tích của hai mặt cầu.
Lời giải:
Gọi bán kính của hình cầu lớn là R và bán kính của hình cầu nhỏ là r.
Ta có R – r = 3 hay R = r + 3.
Thể tích hình cầu lớn là:
V1 = 3⁄4π.r3
Thể tích hình cầu nhỏ là
V2= 3⁄4π.r3
Vì V1 – V2 = 1332π (cm3)
Nên
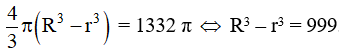
Do đó (r + 3)3 – r3 = 999
⇔ r2+ 3r – 108 = 0.
Giải ra được r1 = –12 (loại), r2 = 9 (chọn).
Do đó bán kính hình cầu nhỏ là 9 cm, bán kính hình cầu lớn là 12 cm.
Diện tích mặt cầu lớn là:
S1 = 4πR2 = 4π . 122 = 576π (cm2).
Diện tích mặt cầu nhỏ là:
S2 = 4πr2 = 4π . 92 = 324π (cm2).
Hiệu diện tích hai mặt cầu là:
S = S1 – S2 = 576π – 324π = 252π (cm2)
Vậy hiệu diện tích hai mặt cầu là 252π cm2.
Ví dụ 3: Một hình cầu có bán kính bằng bán kính đáy của một hình nón. Biết đường sinh của hình nón bằng 12 cm và diện tích xung quanh của hình nón bằng diện tích mặt cầu. Tính thể tích hình cầu.
Lời giải:
Gọi bán kính hình cầu cũng như bán kính đáy hình nón là R.
Diện tích xung quanh hình nón là: πRl = 12πR.
Diện tích mặt cầu là: 4πR2.
Vì diện tích xung quanh hình nón bằng diện tích mặt cầu nên:
12πR = 4πR2 ⇒ R = 3 (cm).
Thể tích hình cầu là:
V1 = 3⁄4π.r3 = 3⁄4π.33 = 36π cm3
Vậy thể tích hình cầu là 36π cm3.
Ví dụ 4: Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ).
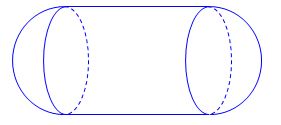
Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là 128π⁄3 m3. Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị m2.
Lời giải
Gọi 4x ( m) là đường sinh hình trụ.
Khi đó đường tròn đáy hình trụ và mặt cầu có bán kính là x (m).
Thể tích bồn chứa nước này chính là thể tích của khối trụ có bán kính đáy R = x;
đường sinh l = h = 4x và thể tích khối cầu có bán kính R= x.
Do đó, thể tích bồn chứa nước là:
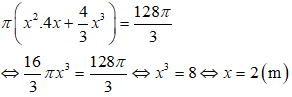
Vậy diện tích xung quanh bồn nước là:
π(4x2 + 2.x.4x) = 48π(m2)
Ví dụ 5: Cho một hình cầu nội tiếp một hình trụ. Chứng minh rằng:
a) Thể tích hình cầu bằng 2⁄3 thể tích hình trụ;
b) Diện tích mặt cầu bằng 2⁄3 diện tích toàn phần hình trụ.
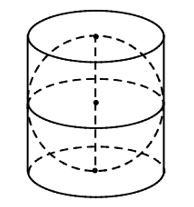
Lời giải:
Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao hình trụ là 2R.
a. Thể tích hình cầu là:
V1 = 3⁄4π.r3
Thể tích hình trụ là
V2 = πR2.h = 2πR3
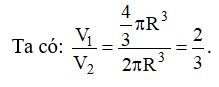
Vậy thể tích hình cầu bằng 2⁄3 thể tích hình trụ.
b) Diện tích mặt cầu là: S1 = 4πR2.
Diện tích hình trụ là: S2 = 2πR(h + R) = 2πR(2R + R) = 6πR2.
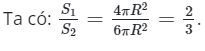
Vậy diện tích mặt cầu bằng 2⁄3 diện tích toàn phần hình trụ.
Bên trên chính là toàn bộ thông tin về công thức tính thể tích khối cầu, diện tích mặt cầu mà chúng tôi đã phân tích chi tiết có thể giúp các bạn hệ thống lại kiến thức để áp dụng vào làm bài tập rồi nhé.




