Như các em đã được biết đường trung tuyến là 1 mảng kiến thức vô cùng quan trọng đối với môn Toán. Nhưng đa số hiện nay trên thế giới còn khá nhiều các bạn học sinh chưa nắm vững được những khái niệm về đường trung tuyến là gì? tính chất đường trung tuyến hay công thức tính đường trung tuyến như thế nào? Trong bài viết dưới đây sẽ giúp các bạn ôn lại những kiến thức tổng quát về đường trung tuyến và những dạng toán thường gặp của đường trung tuyến. Các bạn cùng tham khảo nhé.
Đường trung tuyến là gì?
Đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó.
Đường trung tuyến của một tam giác là đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện trong hình học phẳng. Mỗi tam giác có 3 đường trung tuyến.
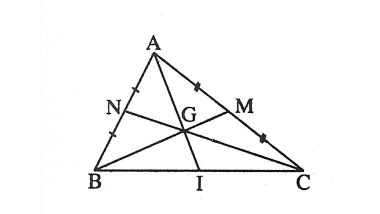
Tính chất đường trung tuyến trong tam giác
- Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
- Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.
- Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Tính chất đường trung tuyến trong tam giác vuông
- Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
- Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
- Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.
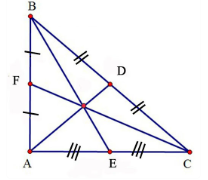
- Tham khảo thêm: Trung bình cộng là gì? Công thức tính trung bình cộng có VD
Tính chất đường trung tuyến trong tam giác đều
- Ba đường trung truyến của tam giác đều sẽ chia tam giác đó thành sáu tam giác có diện tích bằng nhau.
- Trong tam giác đều đường thẳng đi qua một đỉnh bất kì và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.
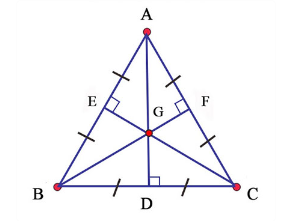
Tính chất đường trung tuyến trong tam giác cân
- Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và chia tam giác thành 2 tam giác bằng nhau.

Công thức tính đường trung tuyến trong tam giác
Công thức tính độ dài đường trung tuyến của cạnh bất kỳ bằng căn bậc 2 của một phần hai tổng bình phương hai cạnh kề trừ một phần tư bình phương cạnh đối.
- ma = √(2b2 + 2c2 – a2)/4
- mb = √(2a2 + 2c2 – b2)/4
- mc = √(2a2 + 2b2 – c2)/4
Trong đó:
- a, b, c: là các cạnh của tam giác.
- ma, mb, và mc là các đường trung tuyến của tam giác.
Các dạng bài tập về đường trung tuyến
Bài 1: Cho tam giác ABC cân ở A có AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM.
a) Chứng minh: AM ⊥ BC;
b) Tính độ dài AM.
Lời giải:
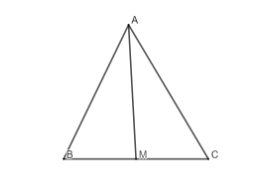
a. Ta có AM là đường trung tuyến tam giác ABC nên MB = MC
Mặt khác tam giác ABC là tam giác cân tại A
Suy ra AM vừa là đường trung tuyến vừa là đường cao
Vậy AM vuông góc với BC
b. Ta có
BC = 16cm nên BM = MC = 8cm
AB = AC = 17cm
Xét tam giác AMC vuông tại M
Áp dụng định lý Pitago ta có:
AC2 = AM2 + MC2 ⇒ 172 = AM2 + 82 ⇒ AM2 = 172 – 82 = 225 ⇒ AM = 15cm
Bài 2: Cho hai đường thẳng x’x và y’y gặp nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho A nằm giữa O và B, AB=2OA. Trên y’y lấy hai điểm L và M sao cho O là trung điểm của đoạn thẳng LM. Nối B với L, B với M và gọi P là trung điểm của đoạn thẳng MB, Q là trung điểm của đoạn thẳng LB. Chứng minh các đoạn thẳng LP và MQ đi qua A.
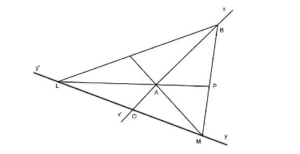
Lời giải :
Ta có O là trung điểm của đoạn LM (gt)
Suy ra BO là đường trung tuyến của ΔBLM (1)
Mặt khác BO = BA + AO vì A nằm giữa O, B hay BO = 2 AO + AO= 3AO vì AB = 2AO (gt)
Suy ra AO= ⅓BO hay BA= ⅔BO (2)
Từ (1) và (2) suy ra A là trọng tâm của ΔBLM ( tính chất của trọng tâm)
mà LP và MQ là các đường trung tuyến của ΔBLM vì P là trung điểm của đoạn thẳng MB (gt)
suy ra các đoạn thẳng LP và MQ đều đi qua A ( tính chất của ba đường trung tuyến)
Bài 3: Cho tam giác ABC với G là trọng tâm. Trên cạnh AG lấy điểm G’ sao cho G là trung điểm của đoạn AG’. Yêu cầu so sánh:
a. Những cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.
b. Những đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.
Lời giải :
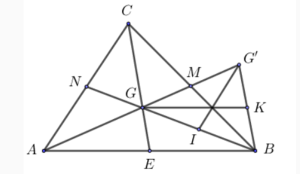
a. Ta có BG cắt AC tại điểm N, CG cắt AB tại điểm E và G là trọng tâm của tam giác ABC.
=> GA = ⅔ AM
Vì G là trung điểm của AG’ => GA =GG’
Suy ra: GG’ = ⅔ AM
Theo giả thuyết ta có G là trọng tâm của tam giác ABC
=> GB = ⅔ BN
Mặt khác: GM = ½ AG (vì G là trọng tâm)
AG = GG’ => GM = ½ GG’
M là trung điểm của đoạn GG’
Vì GM = MG’ và MB = Mc => tam giác GMC = tam giác G’MB
Suy ra: BG’ = CG
Mà CG = ⅔ CE (G là trọng tâm của tam giác ABC)
=> BG’ = ⅔ CE
Vậy mỗi cạnh của tam giác BGG’ bằng ⅔ các đường trung tuyến của tam giác ABC.
b. Ta có BM là đường trung tuyến của tam giác BGG’
mà điểm M lại là trung điểm của đoạn BC nên BM = ½ BC
I là trung điểm của BG => IG = ½ BG
G là trọng tâm tam giác ABC => GN = ½ BG
Suy ra: IG = GN
=> tam giác IGG’ = tam giác NGA theo trường hợp cạnh.góc.cạnh
=>IG’ = AN =>IG’ = ½ AC
Gọi K là trung điểm của đoạn BG => GK là trung tuyến của tam giác BGG’
Mặt khác, vì G là trọng tâm của tam giác ABC => GE = ½ GC
Mà K là trung điểm của BG’ => KG” = EG
Vì tam giác GMC = tam giác G’BM (chứng minh trên)
=> tam giác GCM = tam giác G’BM theo trường hợp góc so le trong
=>CE//BG => tam giác AGE = tam giác AG’B theo trường hợp đồng vị
Do đó tam giác AGE = tam giác GG’K (c.g.c) => AE = GK
Mà AE = ½ AB nên GK = ½ AB
Vậy mỗi đường trung tuyến của tam giác BGG’ bằng ½ các cạnh của tam giác ABC
Bài 4: Cho ΔABC có BM, CN là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME=MG. Kéo dài CN lấy đoạn NF=NG. Chứng minh:
a. EF=BC
b. Đường thẳng AG đi qua trung điểm BC.
Lời giải:
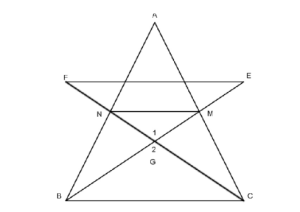
a. Ta có BM và CN là hai đường trung tuyến gặp nhau tại G nên G là trọng tâm của tam giác ΔABC.
⇒GC=2GN
mà FG=2GN⇒GC=GF
Tương tự BG, GE và G1ˆ=G2ˆ (đd). Do đó ΔBGC=ΔEGF(c.g.c))
Suy ra BC=EF
b. G là trọng tâm nên AG chính là đường trung tuyến thứ ba trong tam giác ABC
nên AG đi qua trung điểm của BC.
Bài 5: Cho tam giác ABC có 2 đường đường trung truyến AA’ và BB’ cắt nhau tại điểm O. Yêu cầu: Tính diện tích tam giác ABC, biết diện tích tam giác AOB bằng 5(đvdt)
Lời giải:
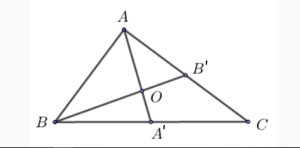
Ta có:
S(AOB) = ⅔ S(AA’B) (vì AO = ⅔ AA’)
S(ABA’) = ½ S(ABC) (vì BA’ = ½ BC)
Từ đó suy ra: S(ABC) = 2S(ABA’) = 3S(AOB)
Theo đề bài ta có: S(AOB) = 5(đvdt) => S(ABC) = 3.5 =15(đvdt).
Bài 6: Cho tam giác ABC vuông ở A, có AB = 18cm, AC = 24cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.
Lời giải:
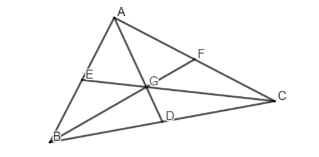
Gọi AD, CE, BF lần lượt là các đường trung tuyến nối từ đỉnh A, C, B của tam giác ABC
Dễ dàng suy ra AE = EB = 9cm, AF = FC = 12cm
Ta có tam giác ABC vuông tại A, áp dụng định lý Pitago ta có:
BC2 = AB2 + AC2 ⇒ BC2 = 182 + 242 = 900 ⇒ BC = 30cm
Ta có ABC vuông mà D là trung điểm cạnh huyền nên AD = BD = DC = 15cm
Suy ra: AG = 2/3 AD = 10cm
Xét tam giác AEC vuông tại A, áp dụng định lý Pitago ta có:
EC2 = AE2 + AC2 ⇒ EC2 = 92 + 242 = 657 ⇒ EC = 3√73 cm ⇒ CG = 2/3 EC = 2√73 cm
Tương tự ta xét tam giác AFB vuông tại A, áp dụng định lý Pitago ta có:
BF2 = AB2 + AF2 ⇒BF2 = 182 + 122 = 468 ⇒ BF = 6√13 cm ⇒ BG = 2/3 BF = 4√13 cm
Tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác là:
AG + BG + CG = 10 + 4√13 + 2√73 (cm)
Như vậy qua bài viết trên, hy vọng với những kiến thức mà chúng tôi vừa trình bày có thể giúp cho bạn nắm chắc và hiểu thêm được phần nào về định nghĩa, tính chất và công thức tính đường trung tuyến để áp dụng giải các bài toán liên quan đến đường trung tuyến để đạt được nhiều thành tích cho bản thân mình nhé!




