Tiếp tục ở phần toán học, Hyundai Smart Phone sẽ chia sẻ lý thuyết về hình chữ nhật là gì, dấu hiệu nhận biết, tính chất hình chữ nhật và diện tích hình chữ nhật và các dạng bài tập từ cơ bản đến nâng cao có đáp án giúp các bạn củng cố lại kiến thức của mình nhé
Định nghĩa hình chữ nhật là gì?
Hình chữ nhật là một hình tứ giác có bốn góc vuông

Tính chất của hình chữ nhật
- Có tất cả các tính chất của hình thang cân và hình bình hành.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường, đồng thời tạo thành 4 tam giác cân.
- Nội tiếp đường tròn có tâm là tâm của hình.
Dấu hiệu nhận biết hình chữ nhật
- Tứ giác có ba góc vuông là hình chữ nhật.
- Hình thang cân có một góc vuông là hình chữ nhật
- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
- Hình bình hành có một góc vuông là hình chữ nhật.
Công thức tính diện tích hình chữ nhật
Diện tích của hình chữ nhật bằng tích chiều rộng nhân với chiều dài hình chữ nhật đó.
S = a.b
Trong đó
- S là diện tích hình chữ nhật
- a là chiều rộng hình chữ nhật
- b là chiều dài hình chữ nhật
Tham khảo thêm:
- Công thức tính chu vi, nửa chu vi hình chữ nhật và bài tập có lời giải
- Hình lập phương là gì? Diện tích xung quanh, toàn phần và thể tích hình lập phương kèm bài tập
- Lý thuyết và công thức tính diện tích, thể tích lăng trụ tam giác đều kèm VD có lời giải
Các dạng bài tập về hình chữ nhật có đáp án
1. Dạng 1: Chứng minh tứ giác là hình chữ nhật
Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình chữ nhật.
Ví dụ 1: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AECH là hình chữ nhật
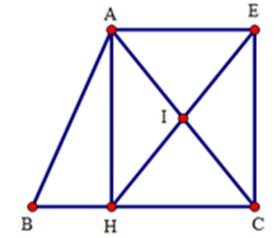
Lời giải
Xét tứ giác AECH có: I là trung điểm của AC (gt); I là trung điểm của HE (do H và E đối xứng nhau qua I)
Do đó AECH là hình bình hành (dấu hiệu nhận biết).
Lại có góc AHC = 900 nên AECH là hình chữ nhật.
Ví dụ 2: Cho hình thang cân ABCD, đáy nhỏ AB = 6, CD = 18, AD = 10. Gọi I, K, M, L lần lượt là trung điểm của các đoạn BC, CA, AD và BD. Tứ giác ABKL là hình chữ nhật
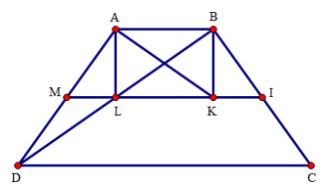
Lời giải
Xét tam giác ABD có: M, L lần lượt là trung điểm của AD, BD, do đó ML là đường trung bình của tam giác ABD.
Suy ra ML//AB và ML = AB/2 = 3
Vậy ML nằm trên đường trung bình MI của hình thang ABCD. (1)
Chứng minh tương tự ta có: IK là đường trung bình của tam giác ABC.
Do đó, IK//AB, IK = AB/2 = 3.
Vậy IK nằm trên đường trung bình MI của hình thang ABCD. (2)
Từ (1) và (2) suy ra: bốn điểm M, L, K, I nằm trên đường trung bình MI của hình thang ABCD.
Ta có:
MI = ½(AB + CD) = ½(6+8) = 12 (do MI là đường trung bình của hình thang ABCD).
Suy ra KL = MI – ML – KI = 12 – 3 – 3 = 6.
Xét tứ giác ABKL có: KL = AB (= 6); KL//AB. Do đó ABKL là hình bình hành.
Lại có:
BL = ½BD, AK = ½AC
Mà AC = BD (đường chéo hình thang cân). Suy ra AK = BL.
Xét hình bình hành ABKL có hai đường chéo AK = BL nên suy ra ABKL là hình chữ nhật.
Ví dụ 3: Cho tam giác ABC vuông tại A, điểm M bất kì trên cạnh BC. Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ M đến AB và AC. Tứ giác ADME là hình gì? Tại sao?
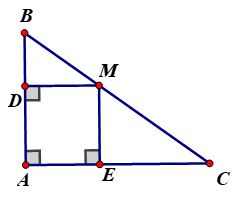
Lời giải
ΔABC vuông tại A nên BAC∧ = 900; mà D thuộc cạnh AB, E thuộc cạnh AC nên DAE∧ = 900
Vì MD ⊥ AB tại D nên ADM∧ = 900
ME ⊥ AC tại E nên AEM∧ = 900
Xét tứ giác ADME có:
DAE∧ = ADM∧ = AEM∧ = 900
Vậy tứ giác ADME là hình chữ nhật (theo dấu hiệu nhận biết).
2. Dạng 2: Vận dụng tính chất của hình chữ nhật để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình chữ nhật và các kiến thức đã học về tứ giác đặc biệt.
Ví dụ 1: Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.
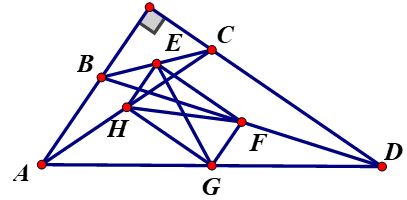
Lời giải
Vì E là trung điểm của BC, H là trung điểm của AC nên EH là đường trung bình của ΔABC
⇒ EH // AB (*) và EH = ½AB (tính chất đường trung bình của tam giác) (1)
Tương tự ta chứng minh được GF là đường trung bình của ΔABD
⇒ GF // AB và GF = ½AB (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) ⇒ HE // GF; HE = GF
⇒ GHEF là hình bình hành (theo dấu hiệu nhận biết) (**)
Mặt khác ta cũng chứng minh được EF là đường trung bình của ΔBCD
⇒ EF // CD (3)
Kết hợp với AB ⊥ CD (gt) (4)
Kết hợp (*), (3) và (4) ⇒ HE ⊥ EF ⇒ HÈ = 900 (***)
Từ (**) và (***) ta có EFGH là hình chữ nhật (theo dấu hiệu nhận biết). Từ đó suy ra hai đường chéo EG = FH (tính chất của hình chữ nhật).
Ví dụ 2: Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn. Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng?
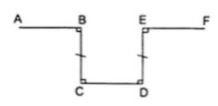
Lời giải
Theo hình, tứ giác BCDE có BC = ED và BC//ED vì cùng vuông góc với CD.
Tứ giác BCDE có hai cạnh đối song song và bằng nhau nên nó là hình bình hành.
Hình bình hành BCDE lại có góc C vuông nên là hình chữ nhật.
Do đó CBE∧ = DEB∧ = 900 ⇒ ABE∧ = BEF∧ = 1800 suy ra A, B, E thẳng hàng và B, E, F cũng thẳng hàng.
Vậy AB, EF cùng nằm trên một đường thẳng.
3. Dạng 3: Sử dụng định lý thuận và đảo của đường trung tuyến ứng với cạnh huyền của tam giác vuông
Phương pháp giải: Sử dụng định lý về tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để tính độ dài đoạn thẳng hoặc chứng minh các hình bằng nhau hoặc chứng minh tam giác vuông.
Ví dụ 1: Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HB = 2 cm, HD = 6 cm. Tính độ dài AB, AD.
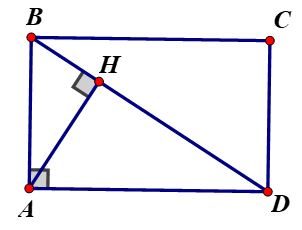
Lời giải:
Ta có: BD = HB + HD = 2 + 6 = 8 cm.
Xét tam giác giác BHA vuông tại H ta có:
BH2 + AH2 = AB2 (định lý Py – ta – go)
⇔ AH2 = AB2 – BH2
⇔ AH2 = AB2 – 22
⇔ AH2 = AB2 – 4 (1)
Xét tam giác AHD vuông tại H ta có:
HD2 + AH2 = AD2 (định lý Py – ta – go)
⇔ AH2 = AD2 – HD2
⇔ AH2 = AD2 – 62
⇔ AH2 = AD2 – 36 (2)
Từ (1); (2) ⇒ AB2 – 4 = AD2 – 36 (3)
Xét tam giác ABD vuông tại A có:
AB2 + AD2 = DB2 (định lý Py – ta – go)
AB2 + AD2 = 82
⇔ AB2 = 64 – AD2 thay vào (3)
⇔ 64 – AD2 – 4 = AD2 – 36
⇔ 2AD2 = 96
⇔ AD2 = 48
⇔ AD = 4√3
=> AB2 = 64 – (4√3)2
⇔ AB2 = 16
⇒ AB = 4 cm
Vậy AD = 4√3 ; AB = 4 cm
Ví dụ 2: Cho hình thang vuông ABCD (A∧=D∧=900) có các điểm E, F thuộc cạnh AD sao cho AE = DF và BFC∧ = 900. Chứng minh DEC∧ = 900
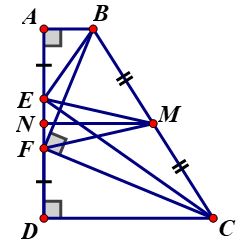
Lời giải
Gọi N là trung điểm của EF
⇒ NE = NF, mà AE = DF (gt)
⇒ AE + NE = DF + NF
⇒ AN = DN
⇒ N là trung điểm của AD
Gọi M là trung điểm của BC
Khi đó: MN là đường trung bình của hình thang ABCD
⇒ MN // AB.
Mặt khác AB ⊥ AD (do hình thang ABCD vuông tại A và D)
Nên MN ⊥ AD ⇒ MN ⊥ EF
Xét ΔMEF có:
- MN là đường cao,
- MN là đường trung tuyến (do N là trung điểm của EF)
⇒ ΔMEF cân tại M nên ME = MF (1)
Lại có:
ΔBFC vuông tại F
M là trung điểm của BC
Nên MF = MB = MC (tính chất trung tuyến ứng với cạnh huyền trong tam giác vuông) (2)
Từ (1) và (2) ⇒ ME = MB = MC.
⇒ ΔBEC vuông tại E (định lý đường trung tuyến ứng với cạnh huyền)
⇒ DEC∧ = 900 (đpcm)
4: Dạng 4. Tìm điều kiện để tứ giác là hình chữ nhật
Phương pháp giải: Vận dụng định nghĩa, tính chất, dấu hiệu nhận biết hình chữ nhật.
Ví dụ: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh EFGH là hình bình hành.
b) Tìm điều kiện của tứ giác ABCD để EFGH là hình chữ nhật.
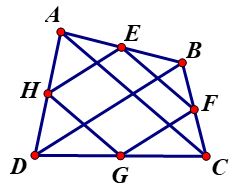
Lời giải:
a) Ta có:
E là trung điểm của AB, H là trung điểm của AD nên HE là đường trung bình của ΔABD
⇒ HE//BD;HE=½BD (1)
F là trung điểm BC, G là trung điểm của DC nên FG là đường trung bình của ΔBCD nên:

Do đó: EFGH là hình bình hành (theo dấu hiệu nhận biết)
b) Giả sử EFGH là hình chữ nhật
⇒ HEF∧ = 900 HE ⊥ EF (3)
Ta có:
E là trung điểm của AB,
F là trung điểm của BC
Do đó: EF là đường trung bình của
⇒ EF //AC (tính chất đường trung bình của tam giác) (4)
Mà HE // BD (chứng minh a) (5)
Từ (3), (4), (5) ⇒ BD ⊥ AC .
⇒ Tứ giác ABCD có 2 đường chéo vuông góc.
Tứ giác ABCD cần có thêm điều kiện hai đường chéo vuông góc thì EFGH là hình chữ nhật.
5. Dạng 5: Tìm diện tích hình chữ nhật
Phương pháp: Áp dụng công thức tính diện tích hình chữ nhật
Ví dụ 1: Diện tích hình chữ nhật thay đổi như thế nào nếu:
a) Chiều dài tăng 2 lần, chiều rộng không đổi?
b) Chiều dài và chiều rộng tăng 3 lần?
c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần?
Lời giải:
Giả sử hình chữ nhật ban đầu có chiều dài là a, chiều rộng là b.
Khi đó diện tích hình chữ nhật là: S = a.b.
a) Chiều dài tăng 2 lần, chiều rộng không đổi
⇒ a’ = 2a, b’ = b
⇒ S’ = a’.b’ = 2a.b = 2ab = 2.S
Do đó diện tích tăng 2 lần.
Vậy diện tích hình chữ nhật tăng 2 lần.
b) Chiều dài và chiều rộng tăng 3 lần
⇒ a’ = 3a; b’ = 3b
⇒ S’ = a’.b’ = 3a.3b = 9ab = 9S
Do đó diện tích tăng 9 lần.
Vậy diện tích hình chữ nhật tăng 9 lần.
c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần
⇒ a’ = 4a; b’ = b/4
⇒ S’ = a’.b’ = 4a.b/4 = ab = S
Do đó diện tích không đổi.
Vậy diện tích hình chữ nhật không đổi.
Ví dụ 2: Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m, có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước 1,2m và 2m. Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sang hay không?
Lời giải:
Diện tích nền nhà: S = 4,2.5,4 = 22,68 (m2)
Diện tích cửa sổ: S1 = 1.1,6 = 1,6 (m2)
Diện tích cửa ra vào: S2 = 1,2.2 = 2,4 (m2)
Diện tích các cửa: S’ = S1 + S2 = 1,6 + 2,4 = 4 (m2)
Ta có: S’/S = 4:22,68 = 17,65% < 20%
Vậy gian phòng không đạt mức chuẩn về ánh sáng.
Ví dụ 3: ABCD là một hình vuông cạnh 12 cm, AE = x cm (h.123). Tính x sao cho diện tích tam giác ABE bằng 1/3 diện tích hình vuông ABCD.
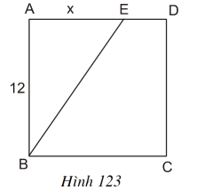
Lời giải
Diện tích tam giác vuông ABE là:
S’ = ½AE.AB = ½x.12 = 6x (cm2)
Diện tích hình vuông là S = 12.12 = 144 cm2
Theo đề bài ta có:
S’ = 1⁄3S = 1⁄3.144 = 48
Suy ra 6x = 48.
Do đó x = 48 : 6 = 8 (cm).
Vậy x = 8 cm.
Ví du 4: Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
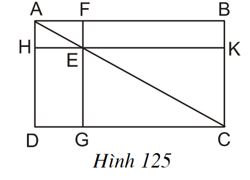
Lời giải
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK
Ta chứng minh: SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = ½AD.DC
SABC = ½AB.BC
Vì ABCD là hình chữ nhật nên AB = CD, AD = BC.
Do đó SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH.
Suy ra AHEF là hình bình hành.
Mà A∧ = 90o
Nên AHEF là hình chữ nhật.
Do đó SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
Ta có: EK // GC, EG // KC.
Suy ra EGCK là hình bình hành.
Mà D∧ = 90o
Nên EGCK là hình chữ nhật.
Do đó SEGC = SEKC (3).
Từ (1), (2) và (3) suy ra: hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Bên trên chính là toàn bộ lý thuyết về hình chữ nhật là gì, dấu hiệu nhận biết, tính chất và công thức tính diện tích hình chữ nhật mà chúng tôi đã phân tích chi tiết có thể giúp bạn nhớ lại kiến thức để áp dụng vào làm bài tập. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi.




