Hình thang cân cũng là một trong những kiến thức hình học thường gặp rất nhiều trong các đề bài kiểm tra và đề thi. Chính vì vậy, các bạn học sinh cần nắm được lý thuyết hình thang cân là gì, dấu hiệu nhận biết, tính chất của hình thang cân và công thức tính chu vi, diện tích hình thang cân thì mới có thể làm bài tập tốt.
Hình thang cân là gì?
Trong hình học Euclid, hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau. Hình thang cân là 1 trường hợp đặc biệt của hình thang.
Ví dụ: ABCD là hình thang cân (đáy AB, CD) ⇔ AB // CD và góc C = góc D
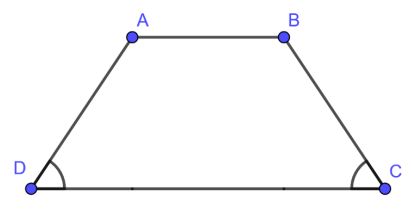
Tính chất của hình thang cân
- Hai cạnh đáy song song với nhau
- Hai cạnh bên bằng nhau.
- Hai góc kề cạnh một đáy bằng nhau.
- Hai đường chéo bằng nhau.
- Hình thang cân nội tiếp đường tròn.
Dấu hiệu nhận biết hình thang cân
- Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Hình thang nội tiếp đường tròn là hình thang cân.
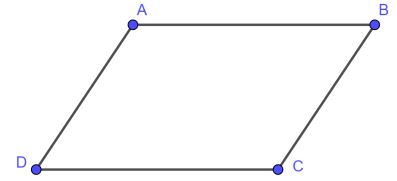
Lưu ý: Hình thang cân thì có hai cạnh bên bằng nhau nhưng hình thang có hai cạnh bên bằng nhau chưa chắc đã là hình thang cân. Ví dụ như hình vẽ dưới đây
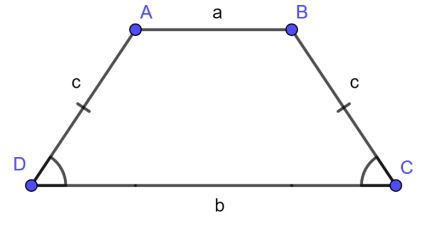
Công thức tính chu vi hình thang cân
P = 2a + b + c
Trong đó:
- P: chu vi hình thang cân
- a: là độ dài của 1 cạnh bên
- b,c: là độ dài của hai cạnh đáy
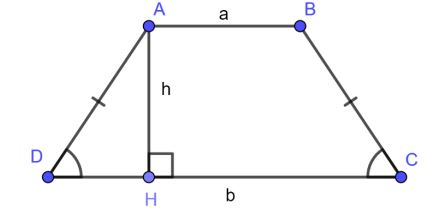
Công thức tính diện tích hình thang cân
Diện tích hình thang bằng chiều cao nhân với trung bình cộng của hai đáy.
S = ½h(a+b)
Trong đó:
- S là diện tích hình thang
- a và b là độ dài của 2 cạnh đáy
- h là độ dài cạnh bên vuông góc với 2 cạnh đáy
Tham khảo thêm:
- Hình thang vuông là gì? Tính chất, Công thức tính chu vi, diện tích hình thang vuông
- Công thức tính chiều cao hình thang cân, vuông và bài tập có đáp án
- Hình thoi là gì? Tính chất, chu vi và diện tích hình thoi kèm VD chuẩn 100%
Các dạng bài tập về hình thang cân có đáp án chi tiết
1. Dạng 1. Tính số đo góc
Phương pháp giải: Sử dụng tính chất hai đường thẳng song song và tổng bốn góc trong một tứ giác kết hợp với kiến thức đã học về hình thang cân
Ví dụ 1: Cho hình thang cân ABCD có AB // CD. Biết A = 2D. Tính các góc của hình thang.
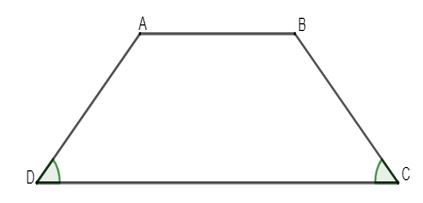
Lời giải
Vì AB // CD ta có:
A∧ + D∧ = 1800 (hai góc trong cùng phía)
Mà A∧ = 2D∧
Nên 2D∧ + D∧ = 1800
⇔3D∧ = 1800
⇒D∧ = 600
⇒ A∧ = 2D∧ = 600.2 = 120
Mà ABCD là hình thang cân nên ta có:
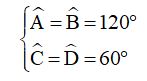
Ví dụ 2: Tính các góc của hình thang cân, biết một góc bằng 50o

Lời giải
Giả sử hình thang ABCD có AB // CD và Dˆ = 50o
Vì Cˆ = Dˆ (tính chất hình thang cân)
⇒ Cˆ = 50o
Lại có: Aˆ + Dˆ = 180o (hai góc trong cùng phía)
⇒ Aˆ = 180o – Dˆ = 180o – 50o = 130o
Mà Bˆ = Aˆ (tính chất hình thang cân)
Suy ra: Bˆ = 130o
2. Dạng 2. Chứng minh hình thang cân
Phương pháp giải: Sử dụng định nghĩa hình thang cân
Ví dụ 1: Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh BCDE là hình thang cân.
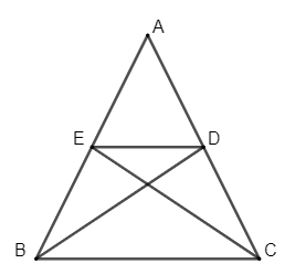
Lời giải
Vì BD là đường trung tuyến của tam giác ABC nên D là trung điểm của AC.
⇒ AD = ½AC
Vì CE là đườg trung tuyến của tam giác ABC nên E là trung điểm của AB
⇒ AE = ½AB
Mà AB = AC (do tam gác ABC cân tại A)
Do đó: AD = AE
Xét tam giác AED có
AD = AE ( chứng minh trên)
Do đó: cân tại A
Ta có:

Mà hai góc này ở vị trí đồng vị nên ED //BC
⇒ Tứ giác BCDE là hình thang
Mặt khác: cân tại A nên ABCˆ = ACBˆ hay EBCˆ = DCBˆ
Vậy hình thang BCDE là hình thang cân (do có hai góc kề một đáy bằng nhau).
Ví dụ 2: Cho tam giác cân ABC cân tại A, các đường phân giác BD, CE (D thuộc AC, E thuộc AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Lời giải
Tam giác ABC cân tại A (giả thiết) nên AB = AC và góc ABC = góc ACB (tính chất tam giác cân)
Vì BD, CE lần lượt là phân giác của góc ABC và góc ACB (giả thiết) nên theo tính chất tia phân giác:
Góc B1 = góc B2 = 1⁄2 của góc ABC
Góc C1 = góc C2 = 1⁄2 của góc ACB
Mà góc ABC = góc ACB (chứng minh trên)
⇒ góc B1 = góc B2 = góc C1 = góc C2
Xét tam giác ABD và tam giác ACE có: (1) AB = AC, (2) Góc A chung, (3) Góc B1 = góc C1 (chứng minh trên)
⇒ tam giác ABD = tam giác ACE (góc – cạnh – góc)
⇒ AD = AE (2 cạnh tương ứng)
Ta có: AD = AE (chứng minh trên) nên tam giác ADE cân tại A (dấu hiêu nhận biết tam giác cân)
⇒ góc AED = góc ADE (tính chất tam giác cân)
Xét tam giác ADE có: góc AED + góc ADE + góc A = 180 độ (định lý tổng ba góc trong một tam giác)
⇒ AED = (180 độ – góc A) / 2 (1)
Xét tam giác ABC có: góc A + góc ABC + góc ACB = 180 độ (định lý tổng ba góc trong một tam giác)
⇒ ABC = (180 độ – góc A) / 2 (2)
Từ (1) và (2) ⇒ góc AED = góc ABC, mà hai góc này là hai góc đồng vị nên suy ra DE // BC.
Do đó BEDC là hình thang.
Lại có góc ABC = góc ACB (chứng minh trên)
⇒ BEDC là hình thang cân.
Ta có: DE // BC ⇒ góc D1 = góc B2 (hai góc so le trong)
Lại có góc B2 = góc B2 (chứng minh trên) nên góc B1 = góc D1
⇒ Tam giác EBD cân tại E
⇒ EB = ED
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
3. Dạng 3. Sử dụng các tính chất của hình thang cân để chứng minh bài toán.
Phương pháp giải: Áp dụng các tính chất về cạnh và góc của hình thang cân đã học để giải quyết bài toán
Ví dụ : Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi G là giao điểm của AD và BC. Gọi F là giao điểm của AC và BD. Chứng minh:
a) Tam giác AGB cân tại G;
b) Các tam giác ABD và BAC bằng nhau;
c) FC = FD.
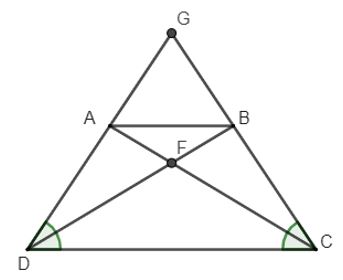
Lời giải
a) Vì AB // CD nên ta có:
GABˆ = ADBˆ (hai góc đồng vị)
GBAˆ = BCDˆ (hai góc đồng vị)
Mà ADCˆ = BCDˆ (do ABCD là hình thang cân)
Do đó: GABˆ = GBAˆ
Xét tam giác AGB có:
GABˆ = GBAˆ
Nên tam giác AGB là tam giác cân tại G.
b) Xét hai tam giác ABD và BAC có:
AB chung
AD = BC (do ABCD là hình thang cân)
AC = BD (do ABCD là hình thang cân)
Do đó: ΔABD = ΔBAC (c – c – c)
c) Ta có:

Suy ra tam giác FCD cân tại F
FC = FD (điều phải chứng minh)
4. Dạng 4: Tính độ dài cạnh, chiều cao, chu vi, diện tích hình thang cân
Phương pháp: Áp dụng công thức tính chu vi, diện tích hình thang cân
Ví dụ 1: Tính độ dài của hình thang có hai cạnh bên bằng nhau biết chu vi của hình thang bằng 68cm và độ dài hai cạnh đáy lần lượt là 20cm và 26cm.
Lời giải
Tổng độ dài hai cạnh bên của hình thang là:
68 – 20 – 26 = 22 (cm)
Độ dài cạnh bên của hình thang là:
22 : 2 = 11 (cm)
Đáp số: 11cm
Ví dụ 2: Một hình thang có chiều cao bằng 56cm. Đáy lớn hơn đáy bé 24cm và đáy bé bằng 2⁄5 đáy lớn. Tính diện tích hình thang.
Lời giải:
Hiệu số phần bằng nhau là:
5 – 2 = 3 (phần)
Độ dài đáy lớn là:
24 : 3 x 5 = 40 (cm)
Độ dài đáy bé là:
40 – 24 = 16 (cm)
Diện tích hình thang là:
(16 + 40) x 56 : 2 = 1568 (cm2)
Đáp số: 1568 cm2
Ví dụ 3: Tính diện tích hình thang có đáy lớn bằng 50 dm và bằng 80% chiều cao, đáy bé kém đáy lớn 12 dm.
Lời giải:
Chiều cao hình thang là:
50 : 100 x 80 = 62,5 (dm)
Đáy bé của hình thang cân là:
50 – 12 = 38 (dm)
Diện tích hình thang đó là:
(50 + 38) x 62,5 : 2 = 2750 (dm2)
Đáp số: 2750 dm2
Ví dụ 4: Thửa ruộng hình thang có trung bình cộng hai đáy là 46 m. Nếu mở rộng đáy lớn thêm 12 m và giữ nguyên đáy bé thì thì được thửa ruộng mới có diện tích lớn hơn diện tích thửa ruộng ban đầu là 114 m². Tính diện tích thửa ruộng ban đầu?
Lời giải
Tổng hai đáy là: 46 x 2 = 92m
Goi chiều cao thửa ruộng là h
Diện tích thửa ruộng ban đầu là: 92 x h : 2 = 46 x h
Tổng đáy lớn và đáy bé sau khi mở rộng đáy lớn thêm 12m là: 92 + 12 = 104m
Diện tích thửa ruộng sau khi mở rộng đáy lớn là: 104 x h : 2 = 52 x h
Thửa ruộng mới có diện tích mới lớn hơn 114m²
Suy ra 52 x h – 46 x h = 114 hay h = 19m
Diện tích thửa ruộng ban đầu là: 46 x 19 = 874m²
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn nắm được hình thang cân là gì, tính chất của hình thang cân và công thức tính chu vi, diện tích hình thang cân để áp dụng vào làm bài tập rồi nhé.




