Tích vô hướng và tích có hướng là phần toán học của chương trình học toán lớp 12. Sau khi học xong các bạn có gặp vấn đề gì chưa hiểu hay khó khăn gì về 2 dạng này thì bài viết này sẽ giúp ích được các bạn rất nhiều. Xem ngay.
Tích có hướng của 2 vectơ là gì? Định nghĩa và tính chất, ứng dụng
Tích có hướng là một phép toán nhị nguyên trên các vectơ trong không gian vectơ ba chiều. Nó là một trong hai phép nhân thường gặp giữa các vectơ (phép toán kia là nhân vô hướng).
Nó khác nhân vô hướng ở chỗ là kết quả thu được là một giả vectơ thay cho một vô hướng. Kết quả này vuông góc với mặt phẳng chứa hai vectơ đầu vào của phép nhân.
1. Định nghĩa:
Trong không gian Oxyz cho hai vecto a→=(a1;a2;a3 ) và b→=(b1;b2;b3 ). Tích có hướng của hai vecto a→ và b→ , kí hiệu là [a→ , b→ ], được xác định bởi
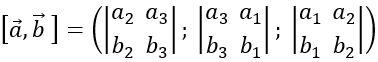
![]()
Chú ý: Tích có hướng của hai vecto là một vecto, tích vô hướng của hai vecto là một số.
Tính chất
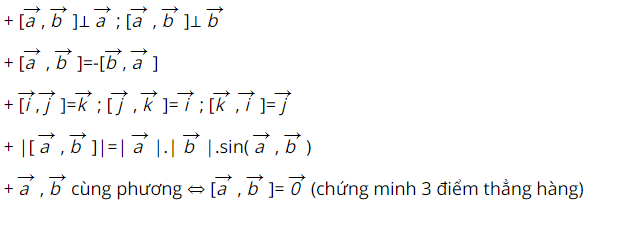
Ứng dụng của tích có hướng
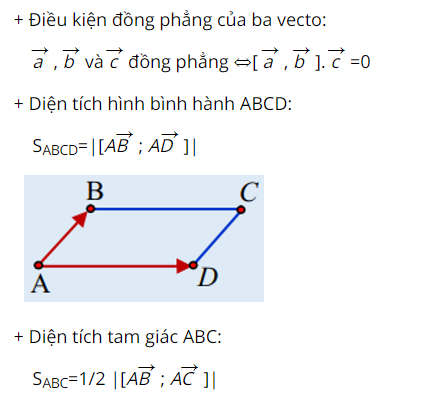
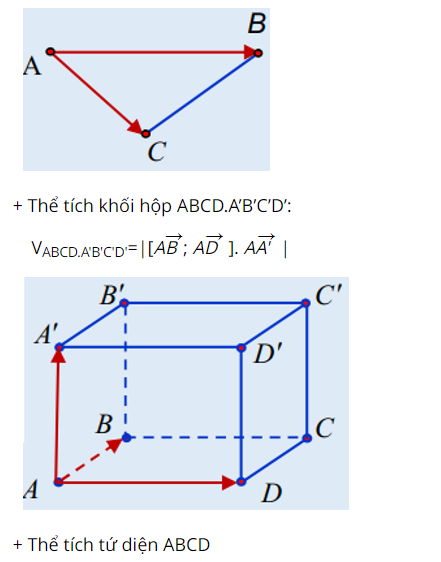
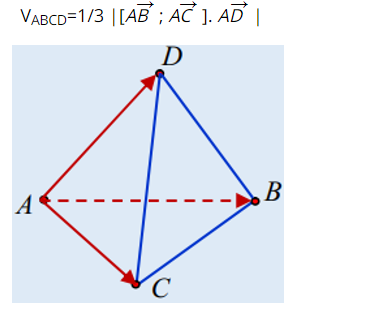
Ví dụ :Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(1; 0; 1), B(-1; 1; 2), C(-1; 1; 0), D(2; -1; -2).
a) Chứng minh rằng A, B, C, D là 4 đỉnh của một tứ diện.
b) Tính thể tích tứ diện ABCD. Suy ra độ dài đường cao của tứ diện qua đỉnh A

Tích vô hướng của 2 vecto là gì? Định nghĩa, tính chất, ứng dụng
Tích vô hướng (tên tiếng Anh: dot product hoặc scalar product) là một phép toán đại số lấy hai chuỗi số có độ dài bằng nhau (thường là các vectơ tọa độ) và cho kết quả là một số. Trong hình học Euclid, tích vô hướng với tọa độ Descartes của hai vectơ thường được sử dụng.
Tích vô hướng cũng thường được gọi là tích trong Euclid dù nó không phải là loại tích trong duy nhất có thể được định nghĩa trong không gian Euclid


=> Hy vọng với chia sẻ của chúng tôi sẽ giúp các bạn hiểu hơn về tích vô hướng cũng như tích có hướng với địa nghĩa, tính chất cũng như ứng dụng nó để giải bài tập tốt nhất.




