Ở phần Toán học hôm nay, Hyundai Smart Phone sẽ chia sẻ định nghĩa, cách chứng minh bất đẳng thức Cosi và các dạng bài tập có lời giải chi tiết giúp các bạn học sinh có thể áp dụng nhanh vào làm bài tập chính xác nhất. Nào chúng ta cùng tìm hiểu nhé
Lý thuyết bất đẳng thức Cosi
1. Định lí
Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng và dấu bằng xảy ra khi và chỉ khi n số đó bằng nhau.
Bất đẳng thức Cô si với 2 số thực không âm:

Dấu “=” xảy ra khi và chỉ khi a = b
Bất đẳng thức Cô si với n số thực không âm:
![]()
Dấu “=” xảy ra khi và chỉ khi x1 = x2 = …= xn
2. Các hệ quả:
Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2
a + 1/a ≥ 2,∀a>0
Nếu x, y cùng dương và có tổng không đổi thì tích (xy) lớn nhất khi và chỉ khi x = y.
Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
Nếu x, y cùng dương và có tích không đổi thì tổng (x + y) nhỏ nhất khi và chỉ khi x = y.
Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.
Xem ngay: Công thức bất đẳng thức Bunhiacopxki và dạng bài tập có lời giải từ A – Z
Chứng minh bất đẳng thức cosi
1. Chứng minh bất đẳng thức Cosi đúng với 2 thực số không âm
Với a = 0 và b = 0 thì bất đẳng thức luôn đúng (1). Ta chỉ cần chứng minh bất đẳng thức luôn đúng với 2 số a, b dương.

⇔ a + b ≥ 2√ab
⇔ a – 2√ab + b ≥ 0
⇔ (√a – √b)2 ≥ 0
(luôn đúng với mọi a, b ≥ 0)
⇒ Bất đẳng thức đã cho luôn đúng với mọi a, b dương (2)
Từ (1) và (2) ⇒ bất đẳng thức cosi đúng với 2 số thực a, b không âm.
2. Chứng minh bất đẳng thức Cosi với 3 thực số không âm
Rõ ràng a = 0, b = 0, c = 0 thì bất đẳng thức luôn đúng. Do đó, ta chỉ cần chứng minh bất đẳng thức đúng với 3 số thực a, b, c dương.
Đặt x = 3√a, y = 3√b, z = 3√c
⇒ x, y, z ≥ 0 ⇒ x + y + z ≥ 0
Bất đẳng thức của 3 số thực a, b, c dương được quy về thành bất đẳng thức của 3 số thực x, y, z dương.
(x + y)3 – 3xy(x+y) + z3 – 3xyz ≥ 0
⇔ (x + y + z)[(x + y)2 – (x + y)z + z2] – 3xy(x + y + z) ≥ 0
⇔ (x + y + z)(x2 + y2 + z2 + 2xy – xz – yz) – 3xy(x + y + z) ≥ 0
⇔ (x + y + z)(x2 + y2 + z2 + 2xy – xz – yz) ≥ 0
⇔ (x + y + z)[(x – y)2 – (y – z)2 + (x – z)2] ≥ 0 (luôn đúng với mọi x, y, z ≥ 0)
Dấu “=” xảy ra khi x = y = z hay a = b = c.
3. Chứng minh bất đẳng thức Cosi với 4 số thực không âm
Dễ dàng nhận ra rằng với a = 0, b = 0, c = 0, d = 0 thì bất đẳng thức luôn đúng. Bây giờ chúng ta chỉ cần chứng minh bất đẳng thức đúng với 4 số thực dương.
Từ kết quả chứng minh bất đẳng thức đúng với 2 số thực không âm ta có:

4. Chứng minh bất đẳng thức Cosi với n số thực không âm
Theo chứng minh ở trên, n = 2 thì bất đẳng thức luôn đúng.
Nếu bất đẳng thức đúng với n số thì nó cũng đúng với 2n số. Chứng minh điều này như sau:
![]()
Theo quy nạp thì bất đẳng thức đúng với n là một lũy thừa của 2.
Mặt khác giả sử bất đẳng thức đúng với n số thì ta cũng chứng minh được nó đúng với n-1 số như sau:
Theo bất đẳng thức cosi cho n số:
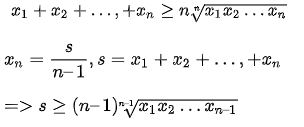
Đây chính là bđt Cosi (n-1) số. Như vậy ta có dpcm.
Tham khảo thêm: Cách tìm vectơ chỉ phương của đường thẳng và bài tập chuẩn 100%
Các dạng bài tập về bất đẳng thức Cosi thường gặp
1. Áp dụng trực tiếp bất đẳng thức Cosi
Ví dụ1: Cho a, b là số dương thỏa mãn a2 + b2 = 2. Chứng minh rằng (a+b)5 ≥ 16ab √(1+a2)(1+b2)
Lời giải:
Ta có (a+b)5 = (a2 + 2ab + b2 )(a3 + 3ab2 + 3a2b + b3)
Áp dụng BĐT cosi ta có:
a2 + 2ab + b2 ≥ 2√2ab(a2 + b2) = 4√ab
(a3 + 3ab2 ) (3a2b+b3) ≥ 2√(a3 + 3ab2 ) (3a2b+b3) = 4√ab (1 + b2)(a2 + 1)
⇒ (a2 + 2ab + b2 )(a3 + 3ab2 + 3a2b + b3) ≥ 16ab√(a2 + 1)( b2 +1)
⇒ Do đó (a + b)5 ≥ 16ab√(a2 + 1)( b2 +1) điều phải chứng minh
Đẳng thức xảy ra khi và chỉ khi a = b = 1
Ví dụ 2: Cho a, b là số dương thỏa mãn a2 + b2 = 2 . Chứng minh rằng:
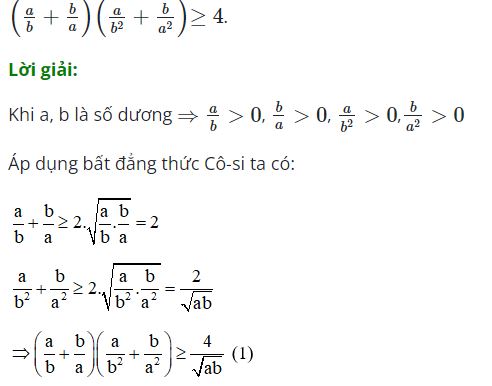
Mặt khác ta có: 2 = a2 + b2 ≥ 2√a2b2 = 2ab
⇒ ab ≤ 1(2)
Từ (1) và (2) ta có:(a/b + b/a)(a/b2 + b/a2) ≥4 (điều cần phải chứng minh)
Đẳng thức xảy ra khi và chỉ khi a = b = 1
Ví dụ 3: Cho hai số dương c, d. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức trong các trường hợp sau:
a) c + d = 6 luôn không đổi, tìm giá trị lớn nhất của biểu thức A = (c + d).cd ;
b) c.d = 5 luôn không đổi, tìm giá trị nhỏ nhất của biểu thức B = c+d/c2d2
Lời giải
a) Ta có: A = (c + d).cd = 6cd vì (c + d) = 6 luôn không đổi.
Áp dụng hệ quả của bất đẳng thức Cô-si ta có:

Vậy giá trị nhỏ nhất của B là 2√5/25 khi c = d = √5
2. Kĩ thuật tách, thêm bớt, ghép cặp
Phương pháp:
- Để chứng minh BĐT ta thường phải biến đổi (nhân chia, thêm, bớt một biểu thức) để tạo biểu thức có thể giản ước được sau khi áp dụng BĐT côsi.
- Khi gặp BĐT có dạng x + y + z ≥ a + b + c (hoặc xyz ≥ abc), ta thường đi chứng minh x + y ≥ 2a (hoặc ab ≤ x2), xây dựng các BĐT tương tự rồi cộng(hoặc nhân) vế với vế ta suy ra điều phải chứng minh.
- Khi tách và áp dụng BĐT côsi ta dựa vào việc đảm bảo dấu bằng xảy ra(thường dấu bằng xảy ra khi các biến bằng nhau hoặc tại biên)
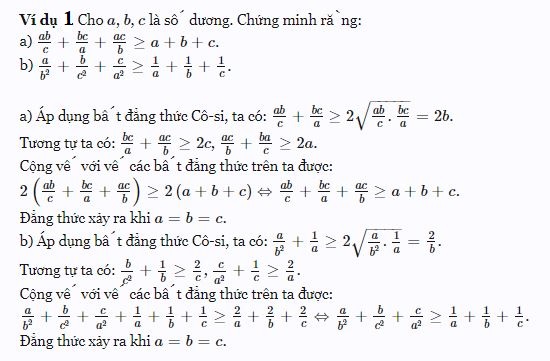
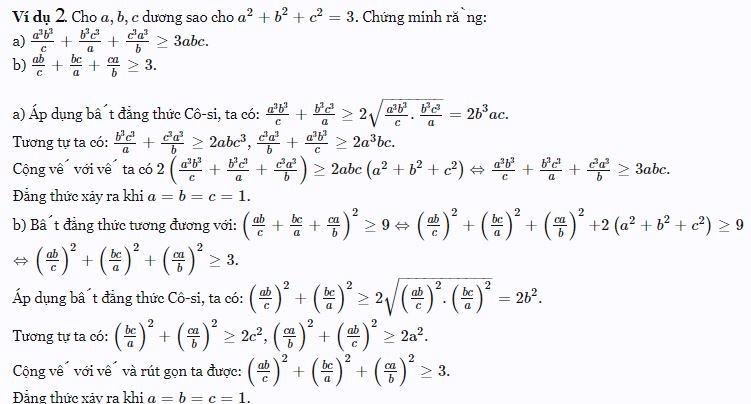
Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn học sinh nắm được lý thuyết về bất đẳng thức Cosi để vận dụng vào làm bài tập rồi nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi.




