Công thức bất đẳng thức Bunhiacopxki và dạng bài tập có lời giải từ A – Z

Trong chuyên đề Toán học hôm nay, Hyundai Smart Phone sẽ chia sẻ lý thuyết và công thức bất đẳng thức Bunhiacopxki kèm theo bài tập minh họa từ cơ bản đến nâng có lời giải để các bạn cùng tham khảo. Nào chúng ta cùng nhau bắt đầu nhé

Bất đẳng thức Bunhiacopxki là gì?

Bất đẳng thức Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, do ba nhà toán học độc lập phát hiện và đề xuất, có nhiều ứng dụng trong các lĩnh vực toán học. Thường được gọi theo tên nhà Toán học người Nga Bunhiacopxki.

Trong lĩnh vực toán học, bất đẳng thức này được ứng dụng khá nhiều để giải các bài toán chứng minh bất đẳng thức và tìm cực trị.

Công thức bất đẳng thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki dạng cơ bản:

(a² + b²)(c² + d²) ≥ (ac + bd)²

Dấu “=” xảy ra khi ac = bd

Bất đẳng thức Bunhiacopxki dạng tổng quát:

Với hai bộ số (a₁, a₂,…,a_n) và (b₁, b₂,…,b_n), ta có:

(a₁₂+a₂₂+…+a²_n).(b₁₂+b₂₂+…+b²_n)≥(a₁b₁+a₂​b₂+…+a_n​b_n​)2

Dấu “=” xảy ra khi a_1⁄b₁ = a₂⁄b₂=…=a_n⁄b_n

Nếu một số nào đó (i = 1, 2, 3,…, n) bằng 0 thì đẳng thức tương ứng bằng 0.

Tham khảo thêm: Lý thuyết về phương trình đường thẳng và các dạng bài tập có lời giải từ A – Z

Chứng minh bất đẳng thức Bunhiacopxki

Ta có:

(a² + b²)(c² + d²) ≥ (ac+bd)²

⇔ (ac)² + (ad)² + (bc)² + (bd)² ≥ (ac)² + 2abcd + (bd)²

⇔ (ad)² + (bc)² ≥ 2abcd

⇔ (ad)² – 1abcd + (bc)² ≥ 0

⇔ (ad – bc)² ≥ 0 (luôn đúng)

Hệ quả của bất đẳng thức Bunhiacopxki

Hệ quả 1:

Hệ quả 2:

Nếu x²₁+…+x²_n = C² (không đổi) thì:

• Max(a₁x₁ +…+ a_nx_n) = C.√a²₁ + …+ a²_n đạt được khi a₁x₁ = … = a_nx_n ≥ 0
• Min(a₁x₁ +…+ a_nx_n) = -C.√a²₁ + …+ a²_n và dấu “=” xảy ra khi a₁x₁ = … = a_nx_n ≤0

Xem ngay: Cách tính delta và delta phẩy của phương trình bậc hai kèm VD

Các dạng bài tập về bất đẳng thức Bunhiacopxki có lời giải

1. Dạng 1: Bất đẳng thức Bunhiacopxki dạng cơ bản

Phương pháp: Bất đẳng thức Bunhiacopxki dạng cơ bản là những bất đẳng thức đánh giá từ đại lượng (a₁b₁ + a₂b₂ + … + a_nb_n)² về đại lượng (a²₁ + a²₂ +…+ a²_n)(b²₁ + b²₂ + …+ b²_n) hoặc ngược lại.

Ví dụ 1. Cho a, b, c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh rằng: 1⁄a + 1⁄b + 1⁄c ≥ 9

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki ta được:

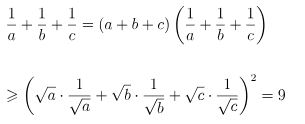
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi a = b = c = 1⁄3

Ví dụ 2: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:

Dấu “=” xảy ra khi và chỉ khi a = b = c

Ví dụ 3: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

(ab + bc + ca – 1)² ≤ (a² + 1)(b² + 1)(c² + 1)

Lời giải

Áp dụng bất đẳng thức Bunhiacopxki ta được:

(ab + bc + ca – 1)²

= [a∙(b + c) + 1∙(bc – 1)]² ≤ (a² + 1)[(b + c)² + (bc – 1)²]

Bài toán quy về chứng minh:

(b + c)² + (bc – 1)² ≤ (b² + 1)(c² + 1)

Đây là một đẳng thức đúng vì:

(b + c)² + (bc – 1)² = (b² + 1)(c² + 1)

Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi

a(bc – 1) = b + c ⇔ a + b + c = abc

2. Dạng 2: Bất đẳng thức Bunhiacopxki dạng phân thức

Phương pháp giải: Bất đẳng thức Bunhiacopxki dạng phân thức là bất đẳng thức có ứng dụng rộng rãi trong chứng minh các bài toán bất đẳng thức. Nó giải quyết được một lớp các bất đẳng thức chứa các đại lượng có dạng phân thức.

Ví dụ 1: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

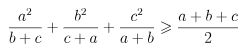
Lời giải

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được:

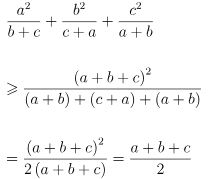
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi a = b = c.

Ví dụ 2: Cho a, b, c là các số thực dương. Chứng minh rằng:

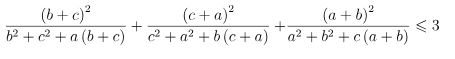
Lời giải

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được:

Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi a = b = c

3. Dạng 3: Dạng thêm bớt

Phương pháp giải: Có những bất đẳng thức (hay biểu thức cần tìm GTLN, GTNN) nếu để nguyên dạng như đề bài cho đôi khi khó hoặc thậm chí không thể giải quyết bằng cách áp dụng bất đẳng thức Bunhiacopxki. Khi đó ta chịu khó biến đổi một số biểu thức bằng cách thêm bớt các số hay biểu thức phù hợp ta có thể vận dụng bất đẳng thức Bunhiacopxki một cách dễ dàng hơn. Ta cùng xem xét các Câu sau để minh họa cho điều đó.

Ví dụ 1. Cho a, b, c là các số dương thỏa mãn ab + bc + ca = 3. Chứng minh rằng:

Lời giải

Bất đẳng thức trên tương đương với

Do đó bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.

Ví dụ 2: Cho a, b, c là các số thực dương thỏa mãn a² + b² + c² = 1. Chứng minh rằng:

Lời giải

Áp dụng bất đẳng thức Cauchy và Bunhiacopxki dạng phân thức ta được:

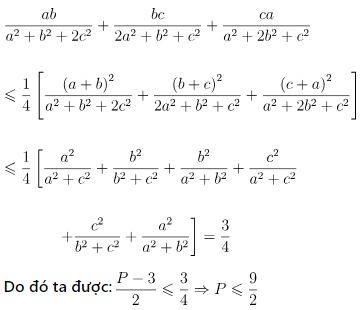
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xảy ra tại a = b = c = √1⁄3

Ví dụ 3: Cho a, b, c là các số thực dương thỏa mãn ab + bc + ca = 3. Chứng minh rằng:

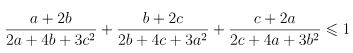
Lời giải

Biến đổi tương đương bất đẳng thức ta được:

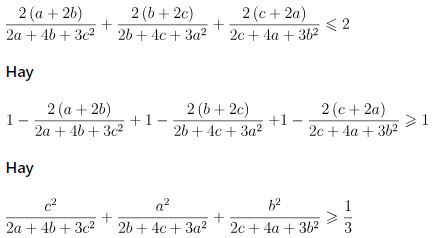
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được:

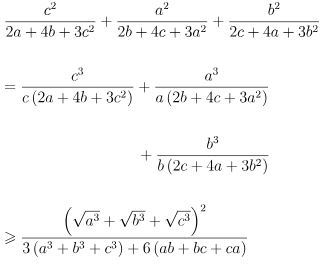
Ta cần chứng minh:

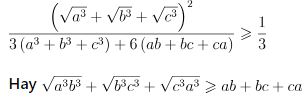
Thật vậy, áp dụng bất đẳng thức Cauchy ta được:

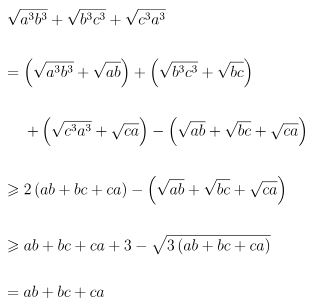
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xảy ra tại a = b = c = 1.

Bên trên chính là toàn bộ lý thuyết và công thức bất đẳng thức Bunhiacopxki mà chúng tôi đã phân tích chi tiết có thể giúp bạn củng cố lại kiến thức của mình để áp dụng vào làm bài tập nhanh chóng và chính xác nhất. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi.