Cách tính delta và delta phẩy của phương trình bậc hai kèm VD

Trong môn Toán, cách tính delta, delta phẩy được áp dụng rất nhiều trong suốt quá trình học tập từ cấp 2 lên cấp 3 nếu các bạn không nắm chắc kiến thức sẽ không giải được các phương trình bậc 2 và bậc 3. Chính vì vậy, Hyundai Smart Phone sẽ hướng dẫn cách cách tính delta, delta phẩy của phương trình bậc 2 kèm theo bài tập minh họa để các bạn cùng tham khảo

Tìm hiểu định nghĩa về delta

Delta là một chữ cái trong bảng chữ Hy Lạp, được kí hiệu là Δ (đối với chữ hoa) và δ (đối với chữ thường). Còn trong toán học, đặc biệt là trong môn Toán lớp 9, ký hiệu Δ thường được sử dụng để biểu thị biệt thức của phương trình bậc hai. Biệt thức Δ được tính bằng công thức Δ = b² – 4ac, trong đó a, b và c là các hệ số trong phương trình bậc hai ax² + bx + c = 0. Giá trị của biệt thức Δ cho ta thông tin về số nghiệm của phương trình bậc hai:

• Nếu Δ > 0, phương trình có hai nghiệm phân biệt.
• Nếu Δ = 0, phương trình có một nghiệm kép.
• Nếu Δ < 0, phương trình không có nghiệm thực.

Delta là ký hiệu cho đường thẳng: Ngoài ra, trong các lớp toán cao hơn, ký hiệu “delta” có thể được sử dụng để đại diện cho đường thẳng. Đây là một ứng dụng khác của chữ cái “delta” trong toán học, và cách sử dụng nó có thể phụ thuộc vào ngữ cảnh cụ thể.

Cách tính delta của phương trình bậc hai chuẩn nhất

Ta xét phương trình: ax² + bx +c = 0, Với biệt thức delta: Δ = b² – 4ac. Sẽ có 3 trường hợp:

• Nếu Δ < 0 thì phương trình vô nghiệm
• Nếu Δ = 0 thì phương trình có nghiệm kép: x₁ = x₂ = -b⁄2a
• Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt: x₁ = (-b + √Δ )/2a và x₂ = (-b – √Δ )/2a

Tham khảo thêm: Trung bình cộng là gì? Công thức tính trung bình cộng kèm VD

Công thức tính delta phẩy của phương trình bậc hai chính xác nhất

Ta xét phương trình: ax² + bx +c = 0. Với biệt thức delta phẩy: Δ′ = b′² – ac. Trong đó: b′ = b/2  được gọi là công thức nghiệm thu gọn.

Tương tự như delta thì delta phẩy chúng ta cũng có 3 trường hợp bao gồm:

• Nếu Δ′ < 0 thì phương trình vô nghiệm
• Nếu Δ′ = 0 thì phương trình có nghiệm kép: x₁ = x₂ = -b’⁄a
• Nếu Δ′ > 0 thì phương trình có hai nghiệm phân biệt: x₁ = (-b’ + √Δ’ )/a và x₂ = (-b’ – √Δ’ )/a

Hệ thức Viet

Cho phương trình bậc 2 một ẩn: ax² + bx + c = 0 (a≠0) (*) có 2 nghiệm x₁ và x₂. Khi đó 2 nghiệm này thỏa mãn hệ thức sau: thì ta có Công thức Vi-et như sau:

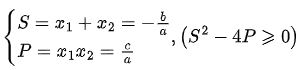
Tham khảo thêm: Ước chung lớn nhất là gì? Cách tìm ước chung lớn nhất kèm bài tập có lời giải

Các dạng bài tập tính delta của phương trình bậc 2 có lời giải

1. Dạng 1. Không dùng công thức nghiệm, giải phương trình bậc hai một ẩn cho trước

Phương pháp: Ta có thể sử dụng một trong các cách sau

• Cách 1: Đưa phương trình đã cho về dạng tích
• Cách 2: Đưa phương trình đã cho về phương trình mà vế trái là một bình phương còn vế phải là một hằng số.

Ví dụ 1:Giải các phương trình sau

a) x² – 6x + 5 = 0

b) 3x² + 12x + 1 = 0

c) – √3x² – 7x = 0

d)- 3/5x² – 7/2 = 0\

Lời giải

a) Ta có: x² – 6x + 5 = 0

⇔ (x – 1)(x – 5) = 0

⇔ x ∈ {1; 5}

b) Ta có: 3x² + 12x + 1 = 0

⇔ 3(x + 2)² = 11

c, Ta có: – √3x² – 7x = 0

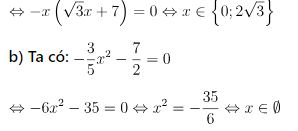
Ví dụ 2: Với giá trị nào của tham số m thì phương trình 4x² + m2x + 4m = 0 có nghiệm x = 1

Lời giải:

Thay x = 1 vào phương trình ta có:

4⋅12 + m2⋅1 + 4m = 0 ⇔ m = –2

Vậy m = −2

Ví dụ 3:

Cho phương trình x² – (2m + 1)x + m² – 2m + 3 = 0 (1). Giải phương trình (1) biết phương trình (1) có một nghiệm x = 2.

Lời giải giải

Vì phương trình có nghiệm x = 2 nên ta có:

22 – (2m + 1)⋅2 + m² – 2m + 3 = 0

⇔ 4 – 4m – 2 + m² – 2m + 3 = 0

⇔ m² – 6m + 5 = 0

⇔ m ∈ {1; 5}

– m = 1 ⇒ x² – 3x + 2 = 0 ⇔ x ∈ {1; 2}

– m = 5 ⇒ x² – 11x + 18 = 0 ⇔ x ∈ {9; 2}

2. Dạng 2. Giải phương trình bậc hai bằng cách sử dụng công thức nghiệm, công thức nghiệm thu gọn

Phương pháp giải: Sử dụng công thức nghiệm, công thức nghiệm thu gọn của phương trình bậc hai để giải.

Ví dụ: Giải các phương trình bậc hai sau:

a) 2x² – 7x + 3 = 0;

b) 6x² + x + 5 = 0;

c) 6x² + x – 5 = 0;

d) 3x² + 5x + 2 = 0;

e) y² – 8y + 16 = 0;

f) 16z² + 24z + 9 = 0.

Lời giải

a) Phương trình bậc hai 2x² – 7x + 3 = 0

Có: a = 2; b = -7; c = 3; Δ = b² – 4ac = (-7)2 – 4.2.3 = 25 > 0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

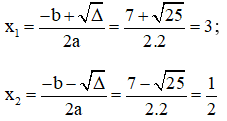
Vậy phương trình có hai nghiệm là 3 và ½

b) Phương trình bậc hai 6x² + x + 5 = 0

Có a = 6; b = 1; c = 5; Δ = b² – 4ac = 12 – 4.5.6 = -119 < 0

Vậy phương trình vô nghiệm.

c) Phương trình bậc hai 6x² + x – 5 = 0

Có a = 6; b = 1; c = -5; Δ = b² – 4ac = 12 – 4.6.(-5) = 121 > 0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

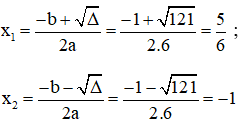
Vậy phương trình có hai nghiệm là -1 và 5/6

d) Phương trình bậc hai 3x² + 5x + 2 = 0

Có a = 3; b = 5; c = 2; Δ = b² – 4ac = 52 – 4.3.2 = 1 > 0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

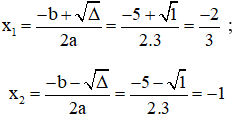
Vậy phương trình có hai nghiệm là -1 và -2/3

e) Phương trình bậc hai y² – 8y + 16 = 0

Có a = 1; b = -8; c = 16; Δ = b² – 4ac = (-8)2 – 4.1.16 = 0.

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép là:

y₁ = y₂ = -b/2a = 8/2.1 = 4

Vậy phương trình có nghiệm kép y = 4.

f) Phương trình bậc hai 16z² + 24z + 9 = 0

Có a = 16; b = 24; c = 9; Δ = b² – 4ac = 242 – 4.16.9 = 0

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép là

z₁ = z₂ = -b/2a = -24/2.16 = -3/4

Vậy phương trình có nghiệm kép z = -3/4

Ví dụ 2: Xác định các hệ số a, b, c ; tính biệt thức Δ rồi tìm nghiệm của các phương trình :

a. 2x² – 5x + 1 = 0

b. 4x² + 4x + 1 = 0

c. 5x² – x + 2 = 0

d. -3x² + 2x + 8 = 0

Lời giải:

a. Phương trình 2x² – 5x + 1 = 0 có a = 2, b = -5, c = 1

Ta có: Δ = b² – 4ac = (-5)² – 4.2.1 = 25 – 8 = 17 > 0

√Δ = √17

Phương trình có 2 nghiệm phân biệt :

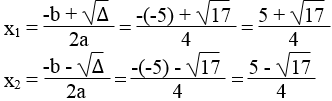
b. Phương trình 4x² + 4x + 1 = 0 có a = 4, b = 4, c = 1

Ta có: Δ = b² – 4ac = 4² – 4.4.1 = 16 – 16 = 0

Phương trình có nghiệm kép : X₁ = x₂ = -b/2a = -4/2.4 = – ½

c. Phương trình 5x² – x + 2 = 0 có a = 5, b = -1, c = 2

Ta có: Δ = b² – 4ac = (-1)² – 4.5.2 = 1 – 40 = -39 < 0

Vậy phương trình vô nghiệm.

d. Phương trình -3x² + 2x + 8 = 0 có a = -3, b = 2, c = 8

Ta có: Δ = b² – 4ac = 2² – 4.(-3).8 = 4 + 96 = 100 > 0

√Δ = √100 = 10

Phương trình có 2 nghiệm phân biệt :

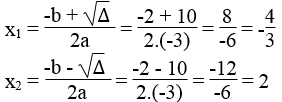
3. Dạng 3. Sử dụng công thức nghiệm, xác định số nghiệm của phương trình dạng bậc hai

Phương pháp giải: Xét phương trình dạng bậc hai: ax² + bx + c = 0.

Lưu ý: Nếu b = 2b’ ta có thể thay điều kiện của ∆ tương ứng bằng ∆’.

Ví dụ 1: Cho phương trình 4x² + 4mx + m + 6 = 0 (1). Tìm m để phương trình (1) có nghiệm kép

Lời giải

Ta có: ∆’ = 4m² – 4m – 24

Phương trình (1) có nghiệm kép ⇔ ∆’ = 0

⇔ 4m² – 4m – 24 = 0

⇔ m2 – m – 6 = 0

⇔ m = –2 ∨ m = 3

Vậy m ∈{–2; 3}.

Ví dụ 2: Cho phương trình mx² + (2m – 5)x + m – 2 = 0 (1) với m ∈ ℝ là tham số. Khi nào

a) Phương trình (1) có nghiệm

b) Phương trình (1) có hai nghiệm phân biệt

Hướng dẫn giải

Xét 2 tường hợp

TH1: Với m = 0 phương trình trở thành –5x – 2 = 0 ⇔ x = -2⁄5
TH2: Với m ≠ 0 phương trình mx² + (2m – 5)x + m – 2 = 0 là một phương trình bậc hai và có

∆ = (2m – 5)² – 4m(m – 2) = –12m + 25

– Nếu ∆ = –12m + 25 > 0 ⇔ m < 25⁄12 thì phương trình có hai nghiệm phân biệt

– Nếu ∆ = –12m + 25 = 0 ⇔ m = 25⁄12 thì phương trình có nghiệm kép x₁ = x₂

Vậy:

a) Phương trình (1) có nghiệm khi và chỉ khi m ≤ 25⁄12

b) Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi m ≠ 0 và m < 25⁄12

Ví dụ 3: Cho phương trình x² + (m – 5)x – 3(m – 2) = 0 với m ∈ ℝ là tham số

a) Chứng minh rằng phương trình trên luôn có nghiệm x = 3 với mọi m ∈ ℝ

b) Tìm m để phương trình có nghiệm kép

c) Tìm m để phương trình có hai nghiệm phân biệt x₁, x₂ thỏa mãn x₁ = 3x²

Hướng dẫn giải

a) Ta có: x² + (m – 5)x – 3(m – 2) = 0

⇔ x² – 3x + (m – 2)x – 3(m – 2) = 0

⇔ x(x – 3) + (m – 2)(x – 3) = 0

⇔ (x – 3)(x + m – 2) = 0

⇔ x = 3 ∨ x = 2 – m

Vậy phương trình trên luôn có nghiệm x = 3 với mọi m ∈ ℝ

b) Phương trình có nghiệm kép khi và chỉ khi hai nghiệm của phương trình trùng nhau

Theo câu a) suy ra: 2 – m = 3 ⇒ m = –1

Ta cũng có thể xét:

∆ = (m – 5)2 + 4⋅3(m – 2)

= m² + 2m + 1 = (m + 1)²

Phương trình có nghiệm kép ⇔ ∆ = 0 ⇔ (m + 1)² = 0 ⇔ m = –1

c) Xét 2 trường hợp

TH1: x₁ = 3 và x₂ = 2 – m

Khi đó: x₁ = 3x² ⇔ 3 = 3(2 – m) ⇔ 2 – m = 1 ⇔ m = 1

TH2: x₁ = −2 và x₂ = 3

Khi đó: x₁ = 3x² ⇔ 2 – m = 3m ⇔ 4m = 2 ⇔ m = ½

4. Dạng 4. Giải và biện luận phương trình dạng bậc hai

Phương pháp giải: Giải và biện luận phương trình dạng bậc hai theo tham số m là tìm tập nghiệm của phương trình tùy theo sự thay đổi của m

Xét phương trình bậc hai dạng: ax² + bx + c = 0 với ∆ = b² – 4ac (hoặc ∆’ = b’² – ac).

• Nếu a = 0, ta đưa về biện luận phương trình bậc nhất
• Nếu a ≠ 0, ta biện luận phương trình bậc hai theo ∆.

Ví dụ 1: Giải và biện luận các phương trình sau (m là tham số)

a) x² + (1 – m)x – m = 0

b) (m – 3)x² – 2mx + m – 6 = 0

Hướng dẫn giải

a) Ta có: ∆ = m² + 2m + 1 =(m + 1)² ≥ 0, ∀m ⇒ √Δ = |m + 1|

∆ = 0 ⇔ m = –1: m Phương trình đã cho có nghiệm kép: x₁ = x₂ = (m-1)/2

∆ > 0 ⇔ m ≠ –1: m Phương trình đã cho có hai nghiệm phân biệt: x₁ = m; x₂ = –1

b) Với m = 3 ⇒ Phương trình có dạng: –6x – 3 = 0 ⇔ x = -½

Với m ≠ 3 ⇒ ∆’ = 9m – 18

∆’ < 0 ⇔ 9m – 18 < 0 ⇔ m < 2: Phương trình vô nghiệm

∆’ = 0 ⇔ 9m – 18 = 0⇔ m = 2: Phương trình có nghiệm kép: x₁ = x₂ = m/(m-3)

Bên trên chính là toàn bộ cách tính delta và delta phẩy của phương trình bậc hai kèm theo các dạng bài tập minh họa có lời giải có thể giúp các bạn củng cố lại kiến thức của mình dể áp dụng vào làm bài tập nhanh nhất và chính xác nhé