Bạn có bài toán yêu cầu tính chỉnh hợp, hóa vị hay tổ hợp nhưng bạn lại không biết cách làm như thế nào bởi bạn không nhớ được công thức tính. Chính vì vậy, Hyundai Smart Phone sẽ chia sẻ công thức hoán vị, chỉnh hợp, tổ hợp kèm theo bài tập có lời giải chi tiết trong bài viết dưới đây
Hoán vị là gì?
Cho tập A gồm n phần tử (n ≥ 1). Khi xếp n phần tử này theo một thứ tự, ta được một hoán vị các phần tử của tập hợp A, (gọi tắt là một hoán vị của A). Kí hiệu số hoán vị của n phần tử là Pn
Ví dụ: Hãy liệt kê tất cả các số tự nhiên gồm ba chữ số khác nhau từ các chữ số 1, 2, 3
Lời giải
Số tự nhiên gồm 3 chữ số khác nhau là: 123; 132; 213; 231; 312; 321
Lưu ý: Hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp
Công thức hoán vị
Pn = n! = n(n – 1)(n – 2)…3.2.1.
Quy ước: 0! = 1; 1! = 1.
Chỉnh hợp là gì?
Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).
Số các chỉnh hợp chập k của một tập hợp có n phần tử là:
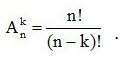
Công thức chỉnh hợp
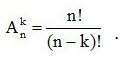
Quy ước: 0! = 1, An0 = 1, Ann = n!
Đặc điểm: Đây là sắp xếp có thứ tự và số phần tử được sắp xếp là k: 0 ≤ k ≤ n.
Xem ngay: Công thức bất đẳng thức Bunhiacopxki và dạng bài tập có lời giải từ A – Z
Tổ hợp là gì?
Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Mỗi tập hợp con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.
Tổ hợp là chọn phần tử không quan trọng thứ tự, số phần tử được chọn là k: 0 ≤ k ≤ n
Công thức tổ hợp
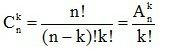
Công thức tính chất của tổ hợp:
- C0n = Cnn = 1
- Ckn = Cn-kn, (0≤k≤n)
- Ck+1n+1 = Ckn + Ck+1n (1≤k≤n)
Tham khảo thêm: Hệ thức lượng trong tam giác vuông, thường kèm bài tập chuẩn 100%
Bài tập về công thức hoán vị, chỉnh hợp, tổ hợp có lời giải
Ví dụ 1: Xếp 10 bạn, trong đó có 5 bạn nam và 5 bạn nữ, vào một ghế dài. Có bao nhiêu cách xếp sao cho:
a) Xếp bất kì
b) Các bạn nam ngồi cạnh nhau
c) Các bạn nam và nữ ngồi xen kẽ với nhau.
Lời giải
a) Số cách xếp 10 bạn vào một ghế dài là một hoán vị của 10: 10!
b) Xếp các bạn nam ngồi cạnh nhau. Ta ghép 5 bạn nam vào 1 “bó”: có 5! cách xếp bên trong “bó”
Rồi xếp 5 bạn nữ cùng 1 “bó” vào ghế dài có: 6! cách xếp.
Vậy có 5! . 6! = 86400 cách xếp sao cho các bạn nam ngồi cạnh nhau.
c) Giả sử xếp 10 bạn vào ghế dài có đánh số thứ tự từ 1 đến 10.
Để xếp xen kẽ các bạn nam và nữ
+ Trường hợp 1: Các bạn nam ngồi vị trí lẻ, các bạn nữ ngồi vị trí chẵn
Số cách xếp các bạn nam: 5!
Số cách xếp các bạn nữ: 5!
Do đó có 5! . 5! cách xếp.
+ Trường hợp 2: Các bạn nam ngồi vị trí chẵn, các bạn nữ ngồi vị trí lẻ
Tương tự như trường hợp trên ta có 5! . 5! cách xếp.
Vậy có 2 . 5! . 5! = 28800 cách xếp.
Ví dụ 2: Có bao nhiêu cách sắp xếp bốn bạn A, B, C, D vào một bàn học gồm 4 chỗ ngồi
Lời giải chi tiết
– Hành động 1: Chọn bạn ngồi vào vị trí 1: 4 cách
– Hành động 2: Chỉ còn 3 bạn
Chọn bạn ngồi vị trí thứ 2: 3 cách
– Hành động 3:Chỉ còn 2 bạn
Chọn bạn ngồi vị trí thứ 3: 2 cách
– Hành động 4: Chỉ còn 1 bạn, chọn bạn để ngồi ở vị trí thứ 4: 1 cách
⇒ Theo quy tắc nhân: 4 . 3 . 2 .1 = 24 cách
Do đó, có 24 cách để xếp 4 bạn vào 4 chỗ ngồi.
Ví dụ 3: Từ các chữ ố 0; 1; 2; 3; 4; 5. Lập được bao nhiêu số tự nhiên sao cho:
a) Số có 6 chữ số khác nhau
b) Số chẵn có 6 chữ số khác nhau
c) Số có 6 chữ số khác nhau có số 1 và 2 đứng cạnh nhau.
Lời giải
a) Lập số có 6 chữ số từ các chữ số: 0; 1; 2; 3; 4; 5
Cách 1: Vị trí đầu tiên (chữ số đầu tiên khác 0): có 5 cách chọn
Các vị trí còn lại là hoán vị của 5 phần tử còn lại: 5!
Vậy có 5 . 5! = 600 số.
Cách 2: Lập số có 6 chữ số khác nhau (kể cả chữ số 0 đứng đầu) là hoán vị của 6: 6!
Lập số có 6 chữ số khác nhau nhưng có chữ số 0 đứng đầu là: 5!
Vậy số có 6 chữ số khác nhau là: 6! – 5! = 600 số.
b) Gọi số abcdef— là số chẵn có 6 chữ số trong các số trên
Vì abcdef— là số chẵn nên f ∈{0; 2; 4}
+ Trường hợp 1: f = 0
Các số a, b, c, d, e là hoán vị của 5 chữ số còn lại: 5! = 120
+ Trường hợp 2: f ∈ {2; 4}
Chọn f: có 2 cách chọn
Chọn a từ các số {1; 2; 3; 4; 5}\{f}: có 4 cách chọn
Chọn b, c, d, e là hoán vị của các chữ số {0; 1; 2; 3; 4; 5}\{a; f}: có 4!
Do đó có 2 . 4 . 4! = 192 số.
Vậy có 120 + 192 = 312 số chẵn có 6 chữ số khác nhau.
c) Để lập được số có 6 chữ số khác nhau có số 1 và 2 đứng cạnh nhau.
Ta ghép 1 và 2 với nhau coi như 1 vị trí.
Giả sử số có 6 chữ số cần lập ở 5 vị trí như hình dưới
| (1) | (2) | (3) | (4) | (5) |
Vị trí đầu tiên có 4 cách chọn (chữ số 1 ghép với 2; 3; 4; 5)
Các vị trí còn lại là hoán vị của 4 chữ số: 4!
Ở vị trí chứa chữ số 1 và 2 có 2! cách xếp chúng.
Vậy có 4 . 4! . 2! = 192 số có 6 chữ số khác nhau và chữ số 1 và 2 đứng cạnh nhau.
Ví dụ 4: Từ các chữ số từ 0 đến 9. Có bao nhiêu cách lập một số tự nhiên sao cho:
a) Số có 6 chữ số khác nhau
b) Số có 6 chữ số khác nhau và chia hết cho 10
c) Số lẻ có 6 chữ số khác nhau.
Lời giải
a) Lập số có 6 chữ số khác nhau
Chọn chữ số đầu tiên từ các số từ 1 đến 9: có 9 cách chọn
Các chữ số còn lại là chỉnh hợp chập 5 của 9 số còn lại (khác chữ số đầu tiên) có A95
Vậy có 9A95 = 136080 số.
b) Số có 6 chữ số khác nhau và chia hết cho 10
Chọn chữ số hàng đơn vị: có 1 cách chọn là chữ số 0
Chọn các chữ số còn lại là chỉnh hợp chập 5 của 9 số còn lại (khác chữ số 0) có A95
Vậy có A95 = 15120 số.
c) Gọi số abcdef— là số lẻ có 6 chữ số khác nhau được lập từ chữ số 0 đến 9
Vì abcdef— là số lẻ nên f ∈{1; 3; 5; 7; 9}
Chọn f: có 5 cách chọn
Chọn a từ các chữ số {1; 2; 3; 4; 5; 6; 7; 8; 9}\{f}: có 8 cách chọn
Chọn b, c, d, e là chỉnh hợp chập 4 của 8 chữ số còn lại (khác f và a): có A84
Vậy có 5.8A84 = 67200 số.
Ví dụ 5: Một tổ gồm 12 học sinh. Có bao nhiêu cách:
a) Chọn ra 2 bạn đại diện cho nhóm
b) Chọn ra 2 bạn, rồi phân công chứ vụ tổ trưởng và tổ phó
c) Chia tổ thành 2 nhóm, trong đó tổ trưởng và tổ phó khác nhóm.
Lời giải
a) Chọn 2 bạn từ 12 bạn là tổ hợp chập 2 của 12: C122 = 66 cách.
b) Chọn 2 bạn rồi phân công chức vị là chỉnh hợp chập 2 của 12: A122 = 132 cách.
c) Chia tổ thành 2 nhóm tức mỗi nhóm có 6 bạn
Trong đó tổ trưởng và tổ phó khác nhóm
Chọn 5 bạn vào cùng nhóm với tổ trưởng trong 10 bạn còn lại: C105 = 252 cách.
Chọn 5 bạn vào cùng nhóm với tổ phó trong 5 bạn còn lại: C55 = 1 cách.
Vậy có 252.1 = 252 cách.
Ví dụ 6: Một hộp có 15 viên bi đỏ và 5 viên bi xanh, 10 viên bi vàng. Có bao nhiêu cách chọn ra 5 viên sao cho
a) Các viên bi cùng màu
b) Số bi xanh bằng số bi đỏ, biết luôn có bi xanh và đỏ
c) Có ít nhất 1 viên bi xanh.
Lời giải
a) Chọn 5 viên bi cùng màu
+ Trường hợp 1: Chọn được 5 viên bi màu đỏ: có C155 = 3003 cách.
+ Trường hợp 2: Chọn được 5 viên bi màu xanh: có C55 = 1 cách.
+ Trường hợp 3: Chọn được 5 viên bi màu xanh: có C105 = 252 cách.
Vậy có 3003 + 1 + 252 = 3256 cách chọn.
b) Chọn được 5 viên bi trong đó số bi xanh bằng số bi đỏ
Trường hợp 1: có 1 viên bi xanh, 1 viên bi đỏ, 3 viên bi vàng:
C51 . C151. C103 = 9000 cách.
Trường hợp 2: có 2 viên bi xanh, 2 viên bi đỏ, 1 viên bi vàng:
C52 . C152. C101 = 10500 cách.
Vậy có 9000 + 10500 = 19500 cách chọn.
c) Chọn được ít nhất 1 viên bi xanh
Số cách chọn 5 viên bi bất kì là:
C305 = 14250 cách.
Số cách chọn 5 viên trong đó không có bi xanh là:
C255 = 53130 cách.
Vậy số cách chọn được ít nhất 1 viên bi xanh là:
142506 – 53130 = 89376 cách chọn.
Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nắm được các công thức hoán vị, chỉnh hợp, tổ hợp để áp dụng vào làm bài tập. Hãy thường xuyên theo dõi chúng tôi để được chia sẻ thông tin bổ ích khác về toán, hóa học, vật lý,..




