Hệ thức lượng trong tam giác là một trong những kiến thức được học ở lớp 9 nhưng lại được sử dụng xuyên suốt trong quá trình học phổ thông. Cho nên, Hyundai Smart Phone sẽ chia sẻ lý thuyết về hệ thức lượng trong tam giác vuông và thường kèm theo bài tập có lời giải chi tiết trong bài viết dưới đây
Các hệ thức lượng trong tam giác
1. Định lí côsin
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai góc còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
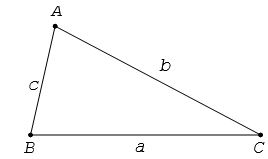
Ta có hệ thức sau:
a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Hệ quả:
- Cos A = (b2 + c2 – a2)⁄2bc
- Cos B = (a2 + c2 – b2)⁄2ac
- Cos C = (a2 + b2 – c2)⁄2ab
2. Định lí sin
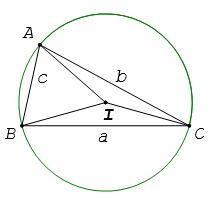
Trong tam giác ABC bất kì, tỉ số giữa cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác. Ta có: a⁄sinA = b⁄sinB = c⁄sinC = 2R. Với R là bán kính đường tròn ngoại tiếp tam giác
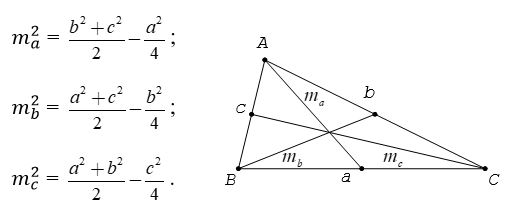
3. Độ dài đường trung tuyến
Cho tam giác ABC có cạnh AB = c, AC = b, BC = a. Gọi độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác ABC là ma, mb, mc Ta có:
Tham khảo thêm: Định nghĩa, tính chất, công thức tính đường trung tuyến kèm VD
4. Công thức diện tích tam giác
Giả sử ha, hb, hc là các đường cao lần lượt kẻ từ đỉnh A, B, C của tam giác ABC. Diện tích tam giác ABC được tính theo một trong các công thức sau:
- S = ½ha.BC = ½hb.AC = ½hc.AB
- S = ½absinC = ½bcsinA = ½casinB
- S = abc/4R
- S = pr
- S = √p(p – a)(p – b)(p – c) (công thức hê – rông)
Với p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC
Hệ thức lượng trong tam giác vuông
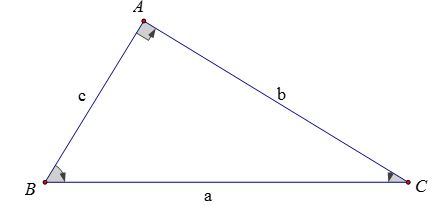
1. Các hệ thức về cạnh và đường cao trong tam giác vuông
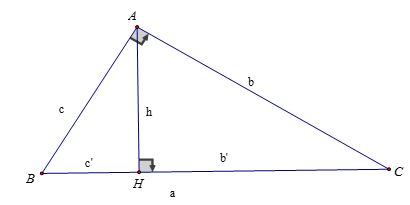
Cho ΔABC, góc A bằng 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:
- BH = c’ được gọi là hình chiếu của AB xuống BC
- CH = b’ được gọi là hình chiếu của AC xuống BC
Khi đó, ta có:
- AB2 = BH.BC hay c2 = a.c’
- AC2 = CH.BC hay b2 = a.b’
- AH2 = CH.BH hay h2 = b’.c’
- AB.AC = AH.BC hay b.c = a.h
- 1⁄AH2 = 1⁄AB2 + 1⁄AC2 hay 1⁄h2 = 1⁄b2 + 1⁄c2
- AB2 + AC2 = BC2 hay b2 + c2 = a2 (Định lý Pytago)
2. Tỉ số lượng giác của góc nhọn
a. Định nghĩa
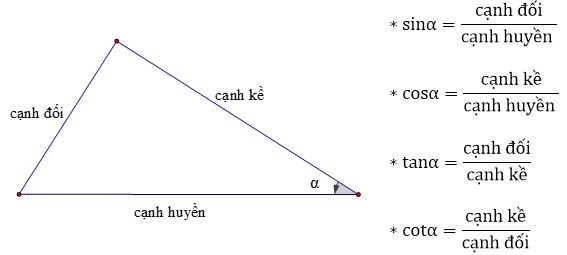
b. Định lí
Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.
c. Một số hệ thức cơ bản
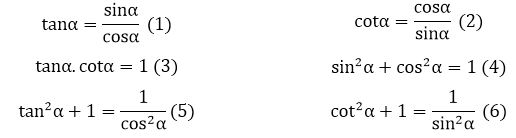
d. So sánh các tỉ số lượng giác
a) Cho α,β là hai góc nhọn. Nếu α < β thì
- sinα < sinβ
- tanα < tanβ
- cosα > cosβ
- cotα > cotβ
b) sinα < tanα; cosα < cotα
3. Hệ thức về góc và cạnh trong tam giác vuông
1. Các hệ thức
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề
b) Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề
- b = a.sinB = a.cosC
- c = a.sinC = a.cosB
- b = c.tanB = c.cotC
- c = b.tanB = b.cotC
Tham khảo thêm: Công thức bất đẳng thức Bunhiacopxki và dạng bài tập có lời giải từ A – Z
Giải tam giác và ứng dụng vào việc đo đạc
Giải tam giác : Giải tam giác là tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
Các bài toán về giải tam giác:
Có 3 bài toán cơ bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh và hai góc.
Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lại
b) Giải tam giác khi biết hai cạnh và góc xen giữa
Đối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ ba
c) Giải tam giác khi biết ba cạnh
Đối với bài toán này ta sử dụng định lí cosin để tính góc
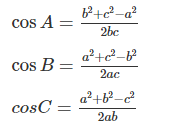
Lưu ý:
- Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)
- Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.
Xem ngay: Công thức tính diện tích tam giác vuông, đều, cần kèm VD có lời giải
Các dạng bài tập về hệ thức lượng trong tam giác có lời giải
Ví dụ 1: Tính x, y trong mỗi hình sau:
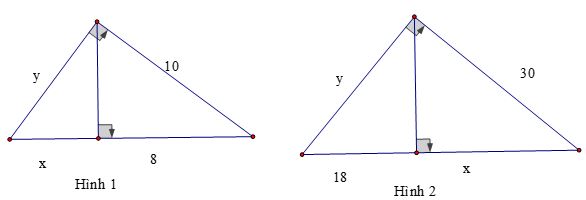
Lời giải
a) x = 4,5 và y = 7,5
b) Áp dụng hệ thức b2 = a.b’ ta được: 302 = x(x + 32)
x2 + 32x – 900 = 0 ⇔ (x – 18)(x + 50) = 0
khi chỉ khi x = 18 hoặc x = -50 (loại)
y2 = 18(18 + 18) ⇒ y = 18√2
Ví dụ 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9cm. Tính độ dài BC và AH
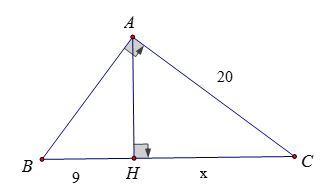
Lời giải:
Đặt HC = x. Áp dụng hệ thức AC2 = BC.HC
⇒ 202 = (9 + x)x
⇔ x2 + 9x – 400 = 0
⇔ (x + 25)(x – 16) = 0
⇔ x = -25 (loại); x = 16
Vậy BC = 16 + 9 = 25 cm
Ta có: AH2 = HB.HC = 9.25 ⇒ AH = 15 (cm)
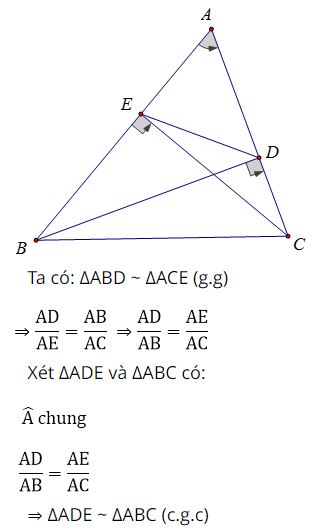
Ví dụ 3: Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Trên HB, HC lần lượt lấy các điểm M, N sao cho góc AMC bằng góc ANB bằng 900. Chứng minh rằng AM = AN
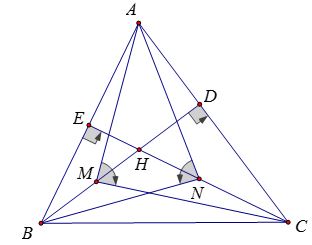
Lời giải
Áp dụng hệ thức b2 = a.b’ vào các tam giác vuông AMC và ANB ta được:
AM2 = AC.AD ; AN2 = AE.AB
ΔABD ~ ΔACE (g.g)
⇒ AB/AC = AD/AE ⇒ AC.AD = AE.AB
⇒ AM2 = AN2 hay AM = AN
Ví dụ 4: Chứng minh rằng giá trị cuả các biểu thức sau không phụ thuộc vào số đo của góc nhọn α
a) A = cos4α + 2cos2α.sin2α + sin4α
b) B = sin4α + cos2α.sin2α + cos2α
Lời giải:
a) A = cos4α + 2cos2α.sin2α + sin4α
=(cos2α + sin2α)2 = 12 = 1
b) B = sin4 α + cos2α.sin2α + cos2α
= sin2α(sin2α + cos2α) + cos2α
= sin2α.1 + cos2α = 1
Ví dụ 5: Cho tam giác ABC, góc A bằng 600. Vẽ các đường cao AD và CE. Chứng minh rằng: BC = 2DE
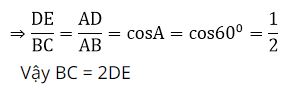
Ví dụ 6: Giải tam giác ABC, biết AB = 4 cm; góc B bằng 600, góc C bằng 450
Lời giải
Vẽ đường cao AH
AH = 2√3 cm; BH = 2cm; CH = 2√3 cm
BC = BH + CH = 2 + 2√3 (cm)
AC = AH/sinC = 2√6 cm
A∧ = 750
Ví dụ 7: Cho tam giác ABC nhọn, BC = a; CA = b; AB = c. Chứng minh rằng: a = b.cosC + c.cosB

Lời giải
Vẽ đường cao AH, điểm H nằm giữa B và C (vì tam giác ABC nhọn)
Xét tam giác ABH vuông tại H có:
BH = AB.cosB = c.cosB
Xét tam giác ACH vuông tại H có:
CH = AC.cosC = b.cosC
⇒ a = BH + CH = c.cosB + b.cosC
Ví dụ 8: Cho tam giác ABC vuông tại A, đường cao AD (D ∈ BC). Gọi E, F theo thứ tự là trung điểm của D trên AB, AC. Chứng minh rằng DB.DC = EA.EB + FA.FC
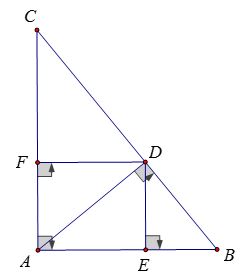
Lời giải
Xét tam giác ADB vuông tại D có DE là đường cao nên
EA.EB = DE2
Xét tam giác ADC vuông tại D có DF là đường cao nên
FA.FC = DF2
⇒ EA.EB + FA.FC = DE2 + DF2 = DE2 + AE2 = AD2
Xét tam giác ABC vuông tại A có AD là đường cao nên
DC.DB = AD2
Do đó: EA.EB + FA.FC = DC.DB
Ví dụ 9: Cho tam giác nhọn ABC. Chứng minh hệ thức: sinA = sinB.cosC + sinC.cosB
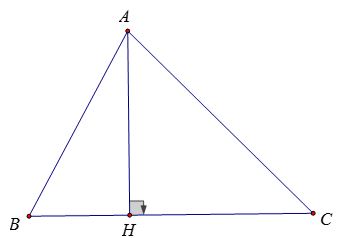
Lời giải:
Vẽ đường cao AH, H nằm giữa B và C
Ta có:

Ví dụ 10: Cho tam giác nhọn ABC, điểm D thuộc cạnh BC sao cho AD = BC. Chứng minh rằng sinA ≥ sinB.sinC
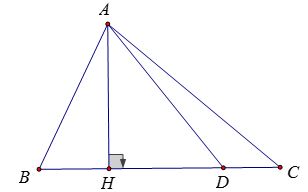
Lời giải:
Vẽ AH vuông góc với BC
Gọi S là diện tích tam giác ABC
Xét các tam giác ABH và ACH vuông tại H, ta có:
AH = AB.sinB = AC.sinC
⇒ AH2 = AB.AC.sinB.sinC
Ta có: AD ≥ AH (dấu bằng xảy ra khi D ≡ H)
Do đó: BC ≥ AH ⇔ BC.AH ≥ AH2 = AB.AC.sinB.sinC (1)
Mặt khác, ta có:
BC.AH = 2S = 2.½ AB.AC.sinA (2)
Từ (1) và (2) ⇒ AB.AC.sinA ≥ AB.AC.sinB.sinC
Hay sinA ≥ sinB.sinC
Dấu bằng xảy ra khi D trùng với H.
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp bạn nắm chắc kiến thức về hệ thức lượng trong tam giác vuông, thường để áp dụng vào làm bài tập rồi nhé




