Tiếp theo Hyundai Smart Phone sẽ chia sẻ tới bạn đọc lý thuyết hình thoi là gì, dấu hiệu nhận biết, tính chất hình thoi và công thức tính chu vi, diện tích hình thoi kèm theo bài tập. Bởi đây là một trong những kiến thức hình học cơ bản của khối lớp 4 nhưng lại được vận dụng xuyên suốt quá trình học đến lớp 12.
Định nghĩa hình thoi là gì?
Hình thoi trong hình học Euclide là một hình tứ giác có 4 cạnh bằng nhau. Đây là hình bình hành với hai đường chéo vuông góc với nhau hay hai cạnh kề bằng nhau.
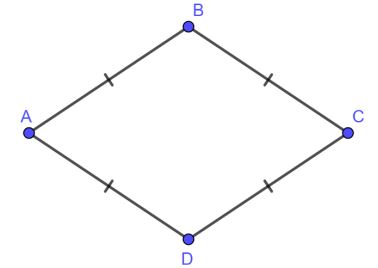
Tính chất của hình thoi
Trong hình thoi, sẽ có những tính chất đặc biệt như:
- Hai đường chéo vuông góc với nhau.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc của hình thoi.
- Hình thoi có tất cả các tính chất của hình bình hành (có cạnh đối song song và bằng nhau; có các góc đối bằng nhau; hai đường chéo cắt nhau tại trung điểm mỗi đường).
Dấu hiệu nhận biết hình thoi
- Tứ giác có bốn cạnh bằng nhau là hình thoi
- Tứ giác có hai đường chéo là đường trung trực của nhau là hình thoi
- Tứ giác có hai đường chéo là đường phân giác của cả bốn góc là hình thoi.
- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Công thức tính chu vi hình thoi
Chu vi của hình thoi được tính bằng tổng độ dài các đường bao quanh hình hay nói cách khác chu vi của hình thoi bằng độ dài một cạnh nhân với 4.
P = a x 4
Trong đó:
- P: là chu vi của hình thoi.
- a: là độ dài của 1 cạnh của hình thoi.
Tham khảo thêm: Công thức tính đường chéo hình thoi và bài tập có lời giải từ A – Z
Công thức tính diện tích hình thoi
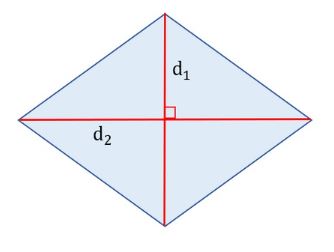
Diện tích hình thoi bằng tích của chiều cao nhân với cạnh đáy tương ứng hoặc diện tích hình thoi bằng một nửa tích hai đường chéo của nó.
S = h x a hoặc S = ½ x (d1 x d2)
Trong đó:
- S: diện tích của hình thoi
- h: độ dài chiều cao của hình thoi
- a: độ dài cạnh đáy tương ứng
- d1, d2 : là độ dài hai đường chéo của hình thoi.
Tham khảo thêm: Hình vuông là gì? Tính chất, chu vi và diện tích hình vuông kèm VD
Hướng dẫn cách vẽ hình thoi
Để có thể vẽ một hình thoi ABCD, chúng ta có thể dùng thước kẻ – eke hoặc thước kẻ – compa. Cụ thể:
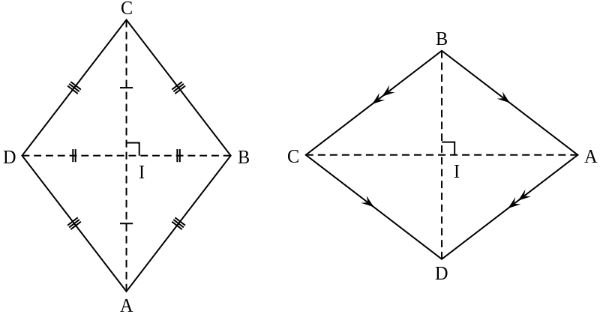
Cách 1 : Vẽ hình thoi bằng thước kẻ và êke
- Bước 1: Vẽ một đoạn thẳng AC với độ dài bất kỳ hoặc cho trước, tiến hành xác định trung điểm O của đoạn thẳng AC.
- Bước 2: Dùng êke vẽ đoạn thẳng BD vuông góc với AC tại O và nhận O là trung điểm của BD.
- Bước 3: Nối các đỉnh A với B, B với C, C với D, D với A ⇒ được hình thoi ABCD.
Cách 2: Vẽ hình thoi bằng thước kẻ và compa
- Bước 1: Vẽ đoạn thẳng AC với độ dài bất kỳ.
- Bước 2: Dùng compa, mở rộng độ mở compa lớn hơn 12 AC. Vẽ cung tròn tâm A và tâm C sao cho hai cung tròn cắt nhau tại hai điểm, hai giao điểm này gọi là B và D.
- Bước 3: Nối các điểm A,B,C,D với nhau ⇒ được hình thoi ABCD.
Xem ngay: Công thức tính diện tích hình quạt tròn, chu vi hình quạt tròn kèm VD
Các dạng bài tập về hình thang có lời giải
1. Dạng 1: Chứng minh tứ giác là hình thoi
Phương pháp giải:
- Cách 1: Chứng minh tứ giác có bốn cạnh bằng nhau.
- Cách 2: Chứng minh tứ giác là hình bình hành có thêm một trong các dấu hiệu: hai cạnh kề bằng nhau, hai đường chéo vuông góc hoặc có một đường chéo là đường phân giác của một góc.
Ví dụ 1. Cho tứ giác ABCD có AC = BD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác EFGH là hình thoi.
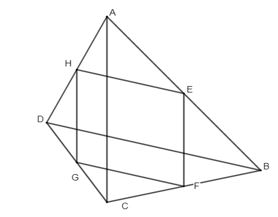
Lời giải:
Vì E là trung điểm của AB, F là trung điểm của BC nên EF là đường trung bình của tam giác ABC
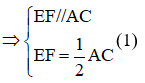
Vì G là trung điểm của DC, H là trung điểm của DA nên HG là đường trung bình của tam giác ADC
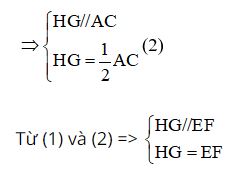
⇒ Tứ giác EFGH là hình bình hành.
Lại có G là trung điểm của DC, F là trung điểm của BC nên GF là đường trung bình của tam giác BCD.
⇒GF = 1⁄2BD
Mà BD = AC
Nên GF = EF
Hình bình hành có hai cạnh kề bằng nhau là hình thoi nên tứ giác EFGH là hình thoi.
Ví dụ 2: Cho hình bình hành ABCD có DC = 2BC. Gọi E, F là trung điểm của AB, DC. Gọi AF cắt DE tại I, BF cắt CE tại K. Tứ giác AEFD là hình thoi.
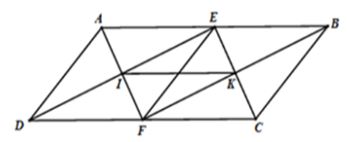
Lời giải
Xét hình bình hành ABCD có E, F lần lượt là trung điểm của AB, CD mà DC = 2BC nên
AE = EB = BC = CF = DF = AD; AB//CD; AD//BC.
Xét tứ giác AEFD có AE = DF; AE//DF nên AEFD là hình bình hành, lại có
AE = AD (cmt) nên hình bình hành AEFD là hình thoi.
Ví dụ 3: Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. Tứ giác AMBM’ là hình thoi
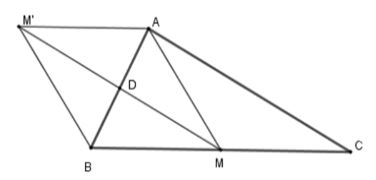
Lời giải
Vì M’ đối xứng M qua D nên DM = DM’.
M, D lần lượt là trung điểm của BC, AB nên MD là đường trung bình của ΔABC . Suy ra MD//AC. (1)
Mặt khác ΔABC vuông ở A nên AB ⊥ AC (2)
Từ (1) và (2) suy ra DM ⊥ AB ⇒ MM’ ⊥ AB
Vì D là trung điểm của AB (gt) và D là trung điểm của MM’ nên tứ giác AMBM’ là hình
bình hành. Mặt khác MM’⊥AB nên AMBM’ là hình thoi.
2. Dạng 2. Vận dụng tính chất của hình thoi để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình thoi
Ví dụ: Cho hình thoi ABCD có B∧ = 600. Kẻ AE ⊥ DC; AF ⊥ BC .
a) Chứng minh AE = AF;
b) Chứng minh tam giác AEF đều.
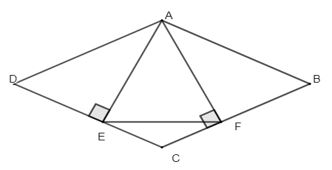
Lời giải
a) Vì ABCD là hình thoi nên ta có:
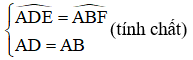
Lại có:
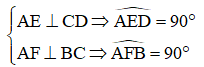
Xét tam giác ADE và tam giác ABF có:
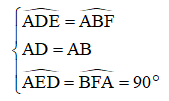
⇒ ΔADE = ΔABF (cạnh huyền – góc nhọn)
⇒ AE = AF (hai cạnh tương ứng)
b) Xét ΔABF vuông tại F ta có:

Xét ΔAEF có:
AE = AF
góc EAF = 600
Do đó: ΔAEF là tam giác đều.
3. Dạng 3. Tìm điều kiện để tứ giác là hình thoi
Phương pháp giải: Vận dụng định nghĩa, các tính chất và dấu hiệu nhận biết của hình thoi
Ví dụ 1: Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình thoi.
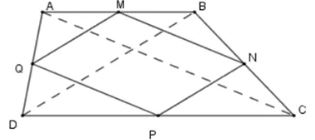
Lời giải:
Xét tam giác ABC có MN là đường trung bình nên
MN//AC, MN = ½ AC (1)
Tương tự ta có PQ là đường trung bình tam giác ADC nên
PQ//AC, PQ = ½ AC (2)
Từ (1) và (2) suy ra MN//PQ, MN = PQ ⇒ MNPQ là hình bình hành.
Để hình bình hành MNPQ là hình thoi ta cần có MN = MQ.
Mà MN = ½AC (cmt); MQ = ½BD
(do MQ là đường trung bình tam giác ABD).
Suy ra AC = BD.
Vậy để hình bình hành MNPQ là hình thoi thì AC = BD hay hình thang ABCD là hình thang cân.
Ví dụ 2: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, BD, AC.
a) Chứng minh tứ giác MPNQ là hình bình hành;
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi?
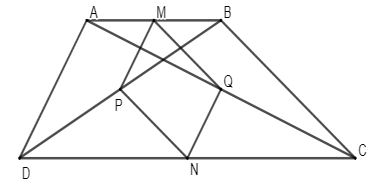
Lời giải:
a) Vì M là trung điểm của AB, P là trung điểm của BD nên MP là đường trung bình của tam giác ABD
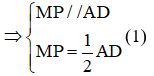
Vì Q là trung điểm của AC, N là trung điểm của DC nên QN là đường trung bình của tam giác ACD
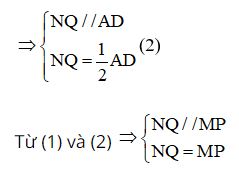
Xét tứ giác MPNQ có:
NQ // MP
NQ = MP
Do đó: tứ giác MPNQ là hình bình hành.
b) Để hình bình hành MPNQ là hình thoi thì MP = MQ
Vì M là trung điểm của AB, Q là trung điểm của AC nên MQ là đường trung bình của tam giác ABC
MQ = ½BC
Để MQ = MP thì ½BC = ½AD hay BC = AD
Vậy để MPNQ là hình thoi thì hình thang ABCD phải có hai cạnh bên AD và BC bằng nhau.
4. Dạng 4: Tính chu vi, diện tích hình thoi
Phương pháp: Áp dụng công thức tính chu vi, diện tích hình thoi
Ví dụ 1: Tính chu vi của hình thoi ABCD có độ dài AB = 5cm.
Lời giải:
Chu vi của hình thoi ABCD là: P = a.4 = 5.4 = 20 (cm)
Ví dụ 2: Hai đường chéo của hình thoi có độ dài 6cm và 8cm. Tính chu vi hình thoi đó.
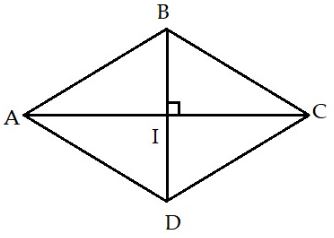
Lời giải:
Gọi I là giao điểm của AC và BD. Khi đó IB = BD : 2 = 3(cm) và IA = AC : 2 = 4(cm)
Xét tam giác vuông IAB có: IA2 + IB2 = AB2 (định lý Pitago)
⟶AB = 5 (cm)
Chu vi của hình thoi ABCD là: 5.4 = 20(cm)
Ví dụ 3: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm, chiều cao hình thoi bằng 3cm. Tính diện tích hình thoi.
Lời giải:
Áp dụng công thức tính diện tích hình thoi khi biết cạnh đáy và chiều cao ta có a = 4cm, h = 3cm.
Diện tích hình thoi ABCD là: 4.3 = 12 (cm2)
Ví dụ 4: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và BACˆ = 600. Diện tích của hình thoi ABCD là ?
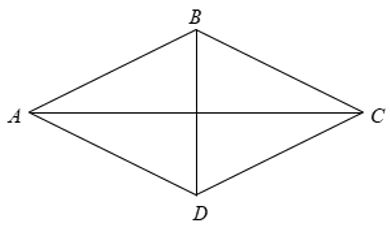
Lời giải:
Xét hình thoi ABCD có BACˆ = 600
Ta có
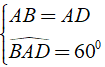
⇒ Δ ABD đều.
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – to – go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 – HB2)
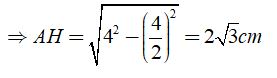
⇒ AC = 2AH = 4√ 3 ( cm )
Do đó SABCD = 1⁄2AC.BD = 1/2.4√ 3 .4 = 8√ 3 ( cm2 )
Ví dụ 5: Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là ?
Lời giải:
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :
AH2 + HB2 = AB2 ⇒ AH = √(AB2 – HB2) = √(102 – 42) = 2√21 ( cm )
⇒ AC = 2AH = 4√ 21 ( cm )
Do đó SABCD = 1⁄2.BD.AC = 1⁄2.4√(21).8 = 16√ 21 ( cm2 )
Bên trên chính là toàn bộ lý thuyết về hình thoi là gì, dấu hiệu nhận biết hình thoi, tính chất hình thoi và công thức tính chu vi, diện tích hình thoi mà chúng tôi đã phân tích chi tiết có thể giúp các bạn củng cố lại kiến thức của mình để vận dụng vào làm bài tập rồi nhé.




