Trong các đề bài kiểm tra hay bài thi có rất nhiều bài tập liên quan đến hình vuông. Do đó, các bạn học sinh cần nắm được hình vuông là gì, tính chất hình vuông, dấu hiệu nhận biết hình vuông và công thức tính chu vi, diện tích hình vuông thì mới có thể làm bài tốt được. Tất cả các kiến thức đã được Hyundai Smart Phone tổng hợp trong bài viết dưới đây
Định nghĩa hình vuông là gì?
Trong hình học Euclid, hình vuông là hình tứ giác đều, có 4 cạnh bằng nhau và 4 góc bằng nhau (4 góc vuông).
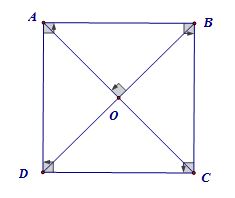
Tính chất của hình vuông
- Hai đường chéo bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường
- Có 2 cặp cạnh song song
- Có 4 cạnh bằng nhau
- Có một đường tròn nội tiếp và ngoại tiếp đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông
- Một đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau
- Giao điểm của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
Dấu hiệu nhận biết hình vuông
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông
- Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông
- Hình thoi có một góc vuông là hình vuông
- Hình thoi có hai đường chéo bằng nhau là hình vuông
- Hình bình hành có một góc vuông và hai cạnh kề bằng nhau.
Công thức tính chu vi hình vuông
Chu vi hình vuông bằng tổng độ dài 4 cạnh của nó nói cách khác dễ hiểu hơn chu vi hình vuông bằng 4 lần độ dài một cạnh
P = 4.a
Trong đó:
- P là chu vi hình vuông.
- a là chiều dài các cạnh hình vuông.
Công thức tính diện tích hình vuông
Muốn tính diện tích hình vuông ta lấy độ dài một cạnh nhân với chính nó. Hay nói cách khác diện tích hình vuông bằng bình phương độ dài của cạnh hình vuông
S = a2
Trong đó:
- S là diện tích hình vuông.
- a là chiều dài các cạnh hình vuông.
Một số cách tính diện tích hình vuông đơn giản khác
Diện tích hình vuông bằng tổng diện tích 2 tam giác vuông cân.
SABCD = ½.a2 + ½.a2
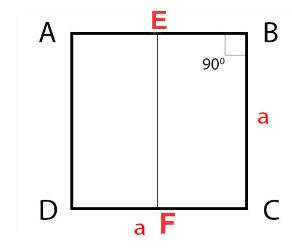
Diện tích hình vuông bằng tổng diện tích 2 hình chữ nhật.
SABCD = SADFE + SEFCB
Tham khảo thêm:
- Công thức tính đường chéo hình vuông và bài tập có lời giải chuẩn 100%
- Hình thang vuông là gì? Tính chất, Công thức tính chu vi, diện tích hình thang vuông
- Công thức tính chu vi, nửa chu vi hình chữ nhật và bài tập có lời giải
Các dạng bài tập về hình vuông có lời giải
1. Dạng 1: Chứng minh tứ giác là hình vuông
Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình vuông.
Ví dụ 1: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Chứng minh tứ giác EFGH là hình vuông.
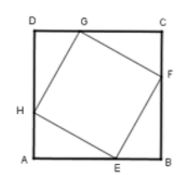
Lời giải

Nên EB = CF = DG = AH
Xét tam giác AHE và tam giác BEF có
A∧ = B∧ = 900
AH = BE (chứng minh trên)
AE = BF (giả thuyết)
Do đó: ΔAHE = ΔBEF (c – g – c)
⇒ HE = EF (hai cạnh tương ứng) (1); AEH∧ = EFB∧ ( hai góc tương ứng)
Xét tam giác CFG và tam giác DGH có
C∧ = D∧ = 900
CF = DG (chứng minh trên)
CG = DH (giả thiết)
Do đó: ΔCFG = ΔDHG (c – g – c)
⇒ FG = GH (hai cạnh tương ứng) (2)
Xét tam giác CFG và tam giác AHE có
Các dạng toán về hình vuông và cách giải
CF = AH(chứng minh trên)
CG = AE (giả thiết)
Do đó: ΔCFG = ΔAHE (c – g – c)
⇒ FG = HE (hai cạnh tương ứng) (3)
Xét tứ giác EFGH ta có:
FG = HE = GH = EF (theo (1), (2), (3))
Nên tứ giác EFGH là hình thoi
Lại có:

Mà hình thoi EFGH có một góc vuông nên hình thoi EFGH là hình vuông.
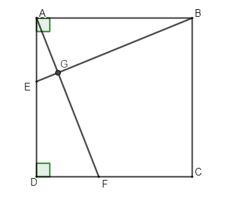
Ví dụ 2: Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác MENF là hình gì? Vì sao?
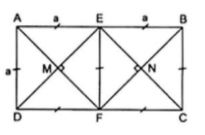
Lời giải
Đặt AD = a thì AB = 2a
Áp dụng tính chất về cạnh và giả thiết vào hình chữ nhật ABCD, ta được:
AE = EB = CF = FD = a.
a) Ta có EF là đường trung bình của hình chữ nhật ABCD nên EF = a
⇒ AE = EF = DF = AD = a
Suy ra tứ giác ADFE có bốn cạnh bằng nhau nên nó là hình thoi.
Hình thoi ADFE có góc DAE = 900 nên nó là hình vuông.
b) Tứ giác MENF là hình vuông
Chứng minh tương tự câu a) ta cũng có tứ giác EBCF là hình vuông.
Áp dụng tính chất về đường chéo vào hai hình vuông ADFE và EBCF, ta được:
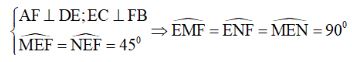
Tứ giác MENF có ba góc vuông nên nó là hình chữ nhật.
Hình chữ nhật MENF lại có EF là đường phân giác của góc MEN nên nó là hình vuông
Ví dụ 3: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F. Tứ giác EFGH là hình gì?
Lời giải
Ta có: ΔABC vuông cân tại A nên

Xét tứ giác EFGH có:

2. Dạng 2: Vận dụng tính chất của hình vuông để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình vuông.
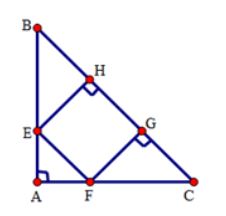
Ví dụ 1: Cho hình vuông ABCD. Trên cạnh AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh:
a) Hai tam giác ADF và BAE bằng nhau;
b) BE vuông góc với AF.
Lời giải
a) Vì ABCD là hình vuông nên AB = AD và D∧ = EAB∧ = 900
Xét hai tam giác ADF và BAE ta có:
AD = AB
D∧ = EAB∧ = 900
AE = DF ( giả thiết)
Do đó: ΔADF = ΔBAE (c – g – c)
b) Gọi giao điểm của BE và AF là G.
Ta có:

Ví dụ 2: Cho hình vuông ABCD. Gọi A là trung điểm của QP.
a) Chứng minh tam giác AMN cân tại A
b) Gọi AF là đường phân giác trong tam giác AMN. Chứng minh AF // MQ // NP
a) Chứng minh tam giác AMN cân tại A
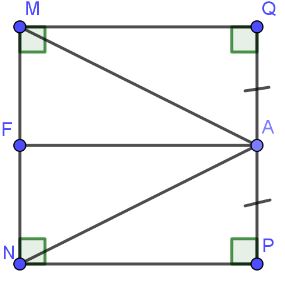
Lời giải
Xét tam giác MAQ và tam giác NAP có
AQ = AP (giả thiết)
Q∧ = P∧ = 900 ( vì MNPQ là hình vuông)
NP = MQ ( vì MNPQ là hình vuông)
ΔMAQ = ΔNAP (c.g.c)
⇒ MA = NA (cạnh tương ứng)
⇒ Tam giác MNA cân tại A (đpcm)
b) Chứng minh AF // MQ // NP
theo phần a, ta có: Tam giác MNA cân tại A
⇒ AF là đường phân giác đồng thời là đường cao
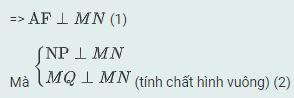
Từ (1) và (2) ⇒ AF // MQ // NP(đpcm)
3. Dạng 3: Tìm điều kiện để tứ giác là hình vuông
Phương pháp giải: Vận dụng định nghĩa và các tính chất và dấu hiệu nhận biết của hình vuông.
Ví dụ: Cho tam giác ABC vuông cân tại A, M là một điểm thuộc cạnh BC. Qua M vẽ các đường thẳng song song với AC, AB chúng cắt các cạnh AB, AC theo thứ tự tại E và F.
a) Tứ giác AFME là hình gì?
b) Xác định vị trí điểm M trên cạnh BC để tứ giác AFME là hình vuông.
Lời giải
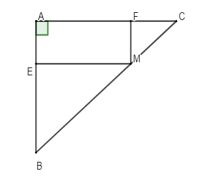
Lời giải
a) Ta có tam giác ABC vuông tại A nên AB ⊥ AC
Vì MF // AB nên MF ⊥ AC ⇒ AFM∧ = 900
Vì ME // AC nên ME ⊥ AB ⇒ AEM∧ = 900
Xét tứ giác AFME có:
AFM∧ = 900
AEM∧ = 900
A∧ = 900
Do đó tứ giác AFME là hình chữ nhật.
b) Để tứ giác AFME là hình vuông thì MF = ME (hình chữ nhật có hai cạnh kề bằng nhau).
Ta có: B∧ = C∧ (do tam giác ABC cân tại A)

Do đó: ΔMFC = ΔMEB (cạnh góc vuông và góc nhọn kề nó)
⇒ MB = MC (hai cạnh tương ứng) hay M là trung điểm của BC.
Vậy để AFME là hình vuông khi M là trung điểm của BC.
4. Dạng 4: Tìm chu vi, diện tích hình vuông
Phương pháp: Áp dụng công thức tính chu vi và diện tích hình vuông
Ví dụ 1: Một miếng đất hình vuông, sau khi mở rộng về một phía thêm 8m thì được một hình chữ nhật có chu vi 116m. Hỏi sau khi mở rộng, miếng đất có diện tích là bao nhiêu?
Lời giải:
Chu vi miếng đất hình vuông là:
116 – 8 x 2 = 100 (m)
Cạnh của miếng đất hình vuông (cũng là chiều rộng của hình chữ nhật) là:
100 : 4 = 25 (m)
Chiều dài miếng đất hình chữ nhật là:
25 + 8 = 33 (m)
Sau khi mở rộng, miếng đất có diện tích là:
25 x 33 = 825 (m2)
Đáp số: 825 (m2)
Ví dụ 2: Một hình vuông có chu vi bằng 36 cm. Người ta kéo dài cạnh của hình vuông đó về bên phải 2 cm . Diện tích của hình sau khi mở rộng là:
Lời giải
Độ dài một cạnh của hình vuông lúc ban đầu là:
36 : 4 = 9 (cm)
Chiều dài của hình chữ nhật mới là:
9 + 2 = 11 (cm)
Diện tích của hình sau khi mở rộng là:
11 × 9 = 99 (cm2 )
Đáp số: 99 cm2 .
Ví dụ 3: Một hình vuông có cạnh 3 dm. Một hình chữ nhật có chiều dài 18 dm và chiều rộng 4 dm. Diện tích của hình vuông bằng một phần mấy diện tích hình chữ nhật?
Lời giải
Diện tích của hình vuông là: 3 × 3 = 9 (cm2 )
Diện tích của hình chữ nhật là: 18 × 4 = 72 (cm2 )
Diện tích hình chữ nhật gấp diện tích hình vuông số lần là: 72 : 9 = 8 (lần)
Diện tích hình vuông bằng 1⁄8.
Đáp số: 1⁄8
Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nắm được hình vuông là gì, dấu hiệu nhận biết hình vuông, tính chất hình vuông và công thức tính chu vi, diện tích hình vuông để áp dụng vào làm bài tập nhé




