Bạn có bài tập tìm thể tích của khối trụ nhưng bạn lại không nhớ công thức tính như thế nào? Đừng lo lắng, sau đây Hyundai Smart Phone sẽ chia sẻ công thức tính thể tích khối trụ kèm theo bài tập có lời giải chi tiết trong bài viết dưới đây
Khối trụ là gì?
Khối trụ là khối có đường bao cong xung quanh và có hai mặt phẳng hình tròn. Khối trụ chỉ có thể lăn về hai phía và xếp chồng được lên nhau.
Công thức tính thể tích khối trụ
Muốn tính thể tích khối trụ ta lấy diện tích mặt đáy nhân với chiều cao của hình trụ. Nói cách khác, thể tích khối trụ bằng chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi.
V = S.h = π.r2.h.
Trong đó:
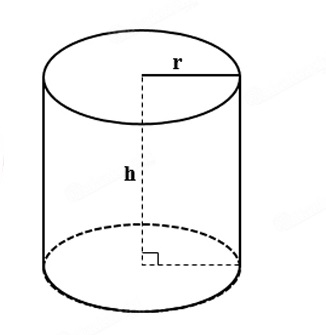
- r là bán kính hình tròn mặt đáy hình trụ
- h là chiều cao của hình trụ
- π là hằng số ( π = 3, 14)
- S là diện tích mặt đáy
Tham khảo thêm: Thể tích khối nón là gì? Công thức tính khối nón tròn xoay, khối nón cụt
Các dạng bài tập về thể tích khối trụ từ cơ bản đến nâng cao
Trong công thức tính thể tích khối trụ có 3 đại lượng đó là thể tích (V), bán kính đáy (r), và chiều cao (h). Chú ý chiều cao h cũng chính bằng độ dài đường sinh của hình trụ. Từ đó ta có 4 dạng toán sau:
Dạng 1: Tìm chiều cao của hình trụ
Phương pháp: Định nghĩa chiều cao hình trụ: Khoảng cách của 2 đáy trên mặt bên. Trong trường hợp chưa biết chiều cao của hình trụ, em có thể lấy thước để đo chính xác độ dài của đường cao rồi thay vào công thức là tính được thể tích của hình trụ.
Ví dụ 1: Một hình trụ (T) có diện tích toàn phần là 120π (cm2) và có bán kính đáy bằng 6 cm. Tính chiều cao của (T)
Lời giải:
Ta có: Stp = 2πrh + 2πr2 = 2π.6.h + 2π.62 = 120π
⇒ h = 4(cm)
Vậy chiều cao của hình trụ là 4 cm.
Ví dụ 2: Một hình trụ có chu vi đáy bằng 20 cm, diện tích xung quanh bằng 14 cm2. Tính chiều cao của hình trụ
Lời giải:
Diện tích xung quanh: Sxq = chu vi đáy x chiều cao = 2πrh = 20 x h = 14
⇒ h = Sxq : chu vi đáy = 14: 20 = 0,7 cm
Ví dụ 3: Một hình trụ (T) có thể tích bằng 81π (cm3) và đường sinh gấp ba lần bán kính đáy. Độ dài đường sinh của (T) là bao nhiêu?
Lời giải:
Gọi bán kính đáy của hình trụ là r
Do đường sinh của hình trụ bằng chiều cao nên chiều cao của hình trụ là 3r
Ta có: V = πr2 h = πr2.3r = 81π ⇒ r = 3
Vậy độ dài đường sinh là 3.3 = 9 cm
Dạng 2: Tìm diện tích đáy tròn
Phương pháp: Để tìm diện tích đáy tròn, ta áp dụng công thức tính diện tích hình tròn: A = π.r2 với A là kí hiệu diện tích đáy tròn, r là bán kính của hình tròn (mặt đáy hình trụ).
Ví dụ: Một hình trụ có diện tích toàn phần gấp 2 lần diện tích xung quanh biết bán kính đáy hình trụ là 6cm. Tính thể tích hình trụ.
Lời giải:
Diện tích toàn phần gấp 2 lần diện tích xung quanh: Stp = 2Sxq
=> 2 x 2 x π x r x h = 2 x π x r x (r + h) => 2h = 6 + h => h = 6 (cm)
Thể tích của hình trụ: V = π x r2 x h = ~ 678,58 cm3
Dạng 3: Tìm bán kính đáy
Phương pháp: Có thể tính bất kì mặt đáy nào vì hai mặt đáy đều bằng nhau. Trong trường hợp chưa biết số đo bán kính đáy, em sử dụng thước để đo khoảng cách rộng nhất trên đường tròn rồi lấy kết quả đó chia cho 2 vì r = ½.d (d là kí hiệu của đường kính).
Ví dụ: Cho khối trụ có thể tích bằng πa³, chiều cao 2a. Tính bán kính đáy của khối trụ.
Lời giải:
Áp dụng công thức: V = π.r2.h
Suy ra:
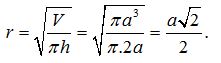
Dạng 4: Tính thể tích hình trụ
Phương pháp: Áp dụng công thức: V = πr2 h
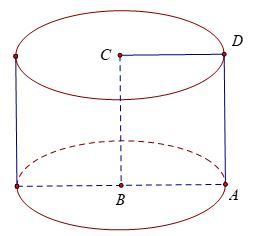
Ví dụ 1: Quay hình vuông ABCD cạnh a xung quanh một cạnh. Thể tích của khối trụ được tạo thành là bao nhiêu?
Lời giải:
Khi quay hình vuông ABCD cạnh a xung quanh một cạnh được hình trụ có chiều cao BC, bán kính BA
V=πr2 h=πa2.a= πa3
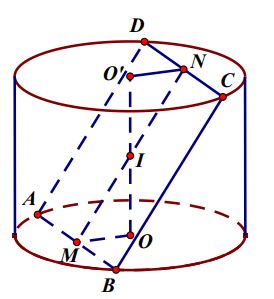
Ví dụ 2: Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45º. Thể tích của khối trụ là?
Lời giải
Lời giải
Gọi M, N lần lượt theo thứ tự là trung điểm của AB và CD.
Khi đó: OM ⊥ AB; O’N ⊥ DC
Giả sử I là giao điểm của MN và OO’
Ta có:
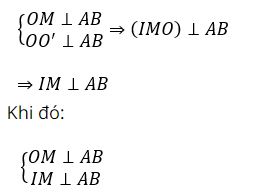
⇒ Góc giữa (ABCD) và đáy là ∠(IMO)=45º
Đặt R = OA, h = OO’.
∆IOM vuông tại O có ∠(IMO)=45º nên ∆IOM vuông cân tại O
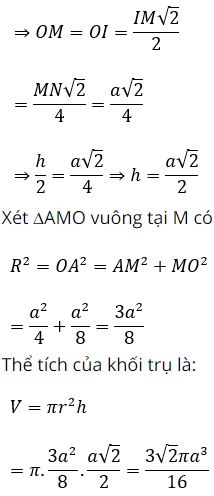
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn nắm được công thức tính thể tích khối trụ để áp dụng vào làm bài tập chính xác nhất. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi




