Lý thuyết và công thức tính diện tích, thể tích lăng trụ tam giác đều kèm VD có lời giải

Ở kiến thức hình học hôm nay, Hyundai Smart Phone sẽ chia sẻ lý thuyết khối lăng trụ tam giác đều là gì và các công thức tính thể tích khối lăng trụ tam giác đều, diện tích xung quanh khối lăng trụ tam giác đều và diện tích toàn khối lăng trụ tam giác đều kèm theo các dạng bài tập có lời giải chi tiết trong bài viết dưới đây

Khối lăng trụ tam giác đều là gì?

Hình lăng trụ tam giác đều là hình lăng trụ có hai đáy là 2 hình tam giác đều

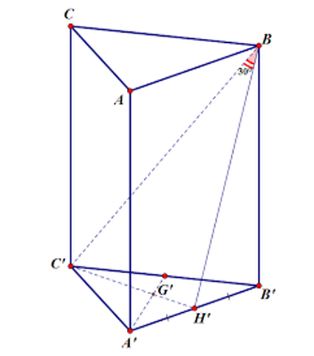
Tính chất của khối lăng trụ tam giác đều

• Hai đáy là hai đa giác đều bằng nhau do đó các cạnh đáy bằng nhau.
• Cạnh bên vuông góc với mặt đáy.
• Các mặt bên là các hình chữ nhật bằng nhau

Công thức tính diện tích xung quanh lăng trụ tam giác đều

Diện tích xung quanh của lăng trụ tam giác đều sẽ bằng tổng diện tích các mặt bên hay bằng tích chu vi đáy và chiều cao

S_xq = p.h

Trong đó:

• S_xq: diện tích xunh quanh hình lăng trụ tam giác đều
• p là chu vi đáy hình lăng trụ tam giác đều
• h là chiều cao hình lăng trụ tam giác đều

Tham khảo thêm: Công thức tính diện tích tam giác vuông, đều, cần kèm VD có lời giải

Công thức tính diện tích toàn phần lăng trụ tam giác đều

Diện tích toàn phần của lăng trụ tam giác đều bằng tổng diện tích các mặt bên và diện tích 2 đáy

S_tp = S_xq + 2S = 3.a.h + a² . (√3)/4

Trong đó:

• S_tp: diện tích toàn phần hình lăng trụ tam giác đều
• a: Độ dài cạnh tam giác đều
• h: Chiều cao hình lăng trụ tam giác đều

Công thức tính thể tích lăng trụ tam giác đều

Thể tích lăng trụ tam giác đều bằng diện tích khối lăng trụ nhân với chiều cao hoặc bằng căn bậc 2 của ba nhân với lập phương tất cả các cạnh bên, sau đó tất cả chia cho 4.

V = S.h = (√3)/4a³h

Trong đó

• V là thể tích hình lăng trụ tam giác đều
• a là chiều dài cạnh đáy của hình lăng trụ tam giác đều
• h là chiều cao của hình lăng trụ tam giác đều

Tham khảo thêm: Thể tích khối nón là gì? Công thức tính khối nón tròn xoay, khối nón cụt

Các dạng bài tập về hình lăng trụ tam giác đều có lời giải

Ví dụ 1: Tính thể tích khối trụ tam giác đều ABCA’B’C’ có độ dài cạnh đáy bằng 8cm và mặt phẳng A’B’C’ tạo với mặt đáy ABC một góc bằng 60 độ.

Đáp án:

Gọi I là trung điểm của đoạn thẳng BC ta có:

AI vuông góc BC (theo tính chất đường trung tuyến của một tam giác đều)

A’I vuông góc BC (Vì A’BC là tam giác cân)

Góc A’BC, ABC = góc AIA’ = 60⁰

⇒ AA’ = AI.tan60⁰ = (8√3/2).√3 = 12 cm

Diện tích tam giác ABC:

S(ABC) = 8√3/4 =  2√3 cm²

Thể tích khối lăng trụ tam giác đều ABCA’B’C’ là:

V = AA’.S(ABC) = 12.2√3 = 24√3 cm³

Ví dụ 2: Cho hình lăng trụ tam giác đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh, toàn phần của hình lăng trụ đứng là?

Lời giải

Diện tích xung quanh hình lăng trụ đứng ABCD.A’B’C’D’ = p x h = (2(AB + BC)) x 2,5 = 45 (cm²).

Diện tích đáy hình chữ nhật ABCD = 4 x 5 = 20 (cm²).

Diện tích toàn phần hình lăng trụ đứng ABCD.A’B’C’D’ = Sxq + 2.S = 45 + 2 x 20 = 85 (cm²).

Ví dụ 3: Tính thể tích lăng trụ đều ABC. A’B’C’, biết (ABC’) hợp với đáy góc 60o và diện tích tam giác ABC’ bằng √3a²

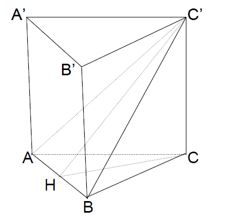
Lời giải

Gọi H là trung điểm AB

Do tam giác ABC là tam giác đều nên CH⊥AB

Tương tự, tam giác C’AB là tam giác cân nên C’H⊥AB

Mà 2 mặt phẳng ( ABC’) và ( ABC) cắt nhau theo giao tuyến AB nên góc giữa hai mặt phẳng ( ABC’) và (ABC) là góc CHC’ = 60⁰

Do diện tích tam giác ABC’ là √3a² nên

½HC’.AB = √3a² ⇔ HC’.AB= 2 √3a² (1)

Xét tam giác HCC’ vuông tại C:

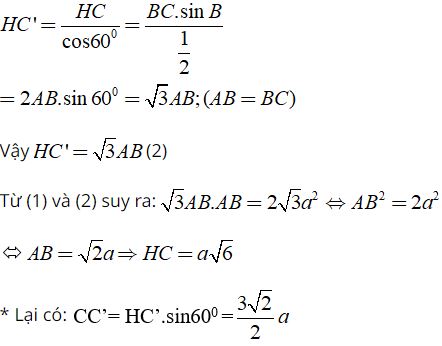
Diện tích tam giác ABC là :

Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nắm được công thức tính thể tích lăng trụ tam giác đều, diện tích xung quanh và diện tích toàn phần của lăng trụ tam giác đều để áp dụng vào làm bài tập chính xác nhé. Cảm ơn các bạn đã theo dõi bài viết của chúng tôi