Ở chuyên mục Toán học hôm nay, Hyundai Smart Phone sẽ chia sẻ lý thuyết phương trình mặt cầu và các dạng bài tập phương trình mặt cầu có đáp án thường gặp trong các đề kiểm tra, thi để các bạn cùng tham khảo và củng cố lại kiến thức của mình nhé
Phương trình mặt cầu là gì?
Cho điểm I cố định và một số thực dương R. Tập hợp tất cả những điểm M trong không gian cách I một khoảng R được gọi là mặt cầu tâm I, bán kính R.
Kí hiệu: S( I;R ) ⇒ S( I;R ) = {M / IM = R}
Có mấy loại phương trình mặt cầu?
Phương trình mặt cầu có 2 dạng chính đó là phương trình tổng quát và chính tắc cụ thể:
1. Phương trình chính tắc
Trong không gian Oxyz, mặt cầu (S) tâm I (a; b; c) và bán kính R có phương trình là:
(S): (x – a)2 + (y – b)2 + (z – c)2 = R2
2. Phương trình tổng quát
Nếu a2 + b2 + c2 – d > 0 thì phương trình sau đây là phương trình tổng quát của (S):
x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 (1)
Tọa độ tâm của (S) có phương trình (1) là I(a;b;c) và bán kính của (S) được tính theo công thức:
R = √a2 + b2 + c2 – d
Cách viết phương trình mặt cầu trong không gian Oxyz
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu I(a, b, c) bán kính R. Khi đó phương trình mặt cầu tâm I(a,b,c) bán kính R có dạng là: (x−a)2+ (b−y)2) + (c−z)2=R2 Hoặc: x2 + y2 + z2 − 2ax − 2cz + d = 0 với a2+ b2+ c2 > d
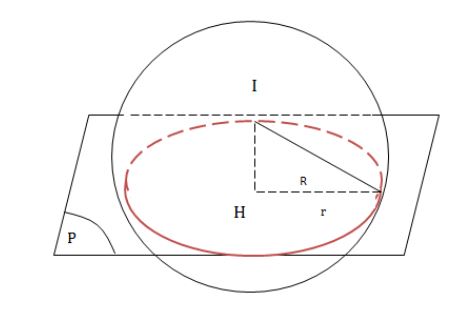
Vị trí tương đối giữa mặt phẳng và mặt cầu
Cho mặt cầu (S): (x−a)2 + (b−y)2 + (c−z)2 = R2 có tâm I, bán kính R và mặt phẳng (P): Ax+By+Cz+D=0.
Ta có:
- d(I,(P)) > R : Mặt phẳng (P) không cắt mặt cầu (S).
- d(I,(P)) = R : Mặt phẳng (P) tiếp xúc với mặt cầu (S).
- d(I,(P)) < R : Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có tâm K là hình chiếu của I trên (P) và bán kính r=√R2−d2(I,(P))
Vị trí tương đối giữa đường thẳng và mặt cầu
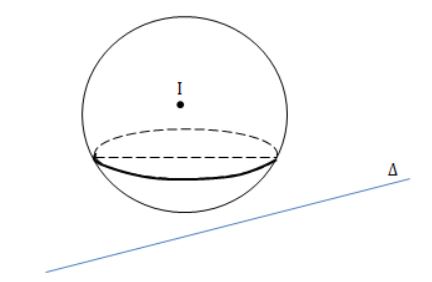
Cho mặt cầu (S): (x−a)2 + (b−y)2 + (c−z)2 = R2 có tâm I, bán kính R và đường thẳng Δ
Ta có khoảng cách d từ mặt cầu (S) đến đường thẳng Δ:
- d > R: Đường thẳng Δ không cắt mặt cầu (S)
- d = R: Đường thẳng Δ tiếp xúc với mặt cầu (S)
- d < R: Đường thẳng Δ cắt mặt cầu (S) theo dây cung AB = √R2 – d2
Tham khảo thêm:
- Lý thuyết về phương trình đường thẳng và các dạng bài tập có lời giải từ A – Z
- Cấp số nhân là gì? Công thức tính cấp số nhân kèm bài tập có đáp án
- Ma trận nghịch đảo là gì? Cách tìm ma trận nghịch đảo 2×2, 3×3, 4×4
Các dạng bài tập về phương trình mặt cầu có lời giải
1. Dạng 1: Xác định tâm và bán kính mặt cầu – Điều kiện để (S) là một mặt cầu.
Phương pháp:
Xét phương trình (S): (x – a)2 + (y – b)2 + (z – c)2 = R2
Khi đó mặt cầu có tâm I (a; b; c), bán kính R
+) Xét phương trình (S) : x2 + y2 + z2 + 2ax + 2by + 2cz + d = 0

Ví dụ 1: Trong không gian hệ trục tọa độ Oxyz, phương trình nào sau đây là phương trình mặt cầu, nếu là phương trình mặt cầu, hãy tìm tâm và bán kính của mặt cầu đó
a) (x-2)2+(y+3)2+z2=5
b) x2+y2+z2-2x+4y-6z+1=0
c) 3x2+3y2+3z2-6x+3y+21=0
Lời giải:
a) Phương trình (x-2)2 + (y+3)2 + z2 = 5 có dạng (x-a)2 + (y-b)2 + (z-c)2 = R2 nên là phương trình mặt cầu có tâm
I (2; -3; 0) và bán kính R=√5.
b) Phương trình x2 + y2 + z2 – 2x + 4y – 6z + 1 = 0 có dạng x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 với a = 1; b = -2; c = 3, d = 1
⇒ a2 + b2 + c2 – d = 13 > 0
Vậy phương trình đã cho là phương trình mặt cầu có tâm I (1; -2; 3) và bán kính R=√13.
c) Phương trình 3x2 + 3y2 + 3z2 – 6x + 3y + 21 = 0
⇔ x2 + y2 + z2 – 2x + y + 7 = 0
Phương trình có dạng x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 với a = 1;b = -1⁄2; c = 0; d = 7
⇒ a2 + b2 + c2 -d = -23⁄4<0
Vậy phương trình đã cho không phải là phương trình mặt cầu.
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x2 + y2 + z2 + 2x – 4y + 6z – 2 = 0. Tính tọa độ tâm I và bán kính R của (S).
Lời giải
Dựa vào phương trình mặt cầu x2 + y2 + z2 + 2x – 4y + 6z – 2 = 0, ta có:
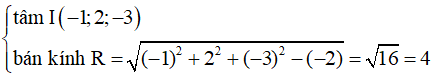
Ví dụ 3: Trong không gian hệ trục tọa độ Oxyz, tìm tất cả các giá trị thực của tham số m để phương trình x2 + y2+ z2 + 2(m+2)x – 2(m-3)z + m2 – 1 = 0 là phương trình của mặt cầu có bán kính nhỏ nhất.
Lời giải:
Phương trình x2 + y2+ z2 + 2(m+2)x – 2(m-3)z + m2 – 1 = 0 có:
a = -(m+2); b = 0; c = m – 3; d = m2 – 1
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ (m+2)2 + (m-3)2– m2 + 1 > 0
⇔ m2 – 2m + 14 > 0
⇔ m ∈ R.
Khi đó, bán kính mặt cầu là:
R = √m2 – 2m + 14 = √(m – 1)2 + 13 ≥ √13
Dấu bằng xảy ra khi m = 1.
Vậy với m = 1 thì mặt cầu có bán kính nhỏ nhất R=√13.
2. Dạng 2: Viết phương trình mặt cầu khi biết tâm và bán kính
Phương pháp giải:
- Bước 1: Xác định tâm I (a; b; c).
- Bước 2: Xác định bán kính R của (S).
- Bước 3: Thế vào phương trình (S):
Dạng phương trình mặt cầu (S) có tâm I (a; b; c) và bán kính R. (S): (x – a)2 + (y – b)2 + (z – c)2 = R2
Ví dụ 1: Trong không gian Oxyz cho điểm A (-1; 2; 0), viết phương trình mặt cầu tâm A bán kính bằng 4
Lời giải
Dạng phương trình mặt cầu (S) : (x – a)2 + (y – b)2 + (z – c)2 = R2
Tâm là A suy ra a = -1, b = 2, c = 0 và R = 4
Thế vào phương trình mặt cầu (S) ta được (S): (x + 1)2 + (y – 2)2 + z2 = 16
Ví dụ 2: Viết phương trình mặt cầu có đường kính AB với A (4; -3; 7), B(2; 1; 3)
Lời giải:
Gọi I là trung điểm của AB
Do AB là đường kính của mặt cầu I là tâm mặt của mặt cầu.
⇒ I(3; -1;5)
Bán kính mặt cầu là:
R = IA = √(4-3)2 + (-1 + 3)2 + (5 – 7)2 = 3
Vậy phương trình mặt cầu có đường kính AB là:
(x-3)2 + (y+1)2 + (z-5)2 = 9
3. Dạng 3: Viết phương trình mặt cầu biết tâm và tiếp xúc với mặt phẳng
Phương pháp giải: Cho điểm I (a; b; c) và mặt phẳng (P): Ax + By + Cz + D = 0. Vì mặt cầu tiếp xúc với mặt phẳng nên ta có:
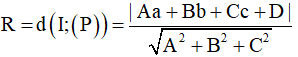
Từ đó viết được phương trình mặt cầu tâm I và bán kính R đã tính phía trên
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho điểm A (2; 1; 1) và mặt phẳng (P): 2x – y + 2z + 1 = 0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P)
Lời giải
Vì mặt cầu tâm A tiếp xúc với mặt phẳng (P) nên bán kính của mặt cầu là
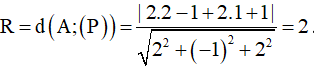
Vậy phương trình mặt cầu là: (x – 2)2 + (y – 1)2 + (z – 1)2 = 4
Ví dụ 2: Cho điểm A (1; 2; 4) và mặt phẳng (P): x + y + z =1. Viết phương trình mặt cầu (S) có tâm A, biết mặt cầu (S) cắt mặt phẳng (P) theo một thiết diện là một đường tròn có chu vi 4π
Lời giải:
Gọi r là bán kính thiết diện
Theo bài ra, đường tròn thiết diện có chu vi 4π
⇒ 2πr = 4π ⇒ r = 2
Phương trình mặt phẳng (P): x + y + z – 1 = 0
Khoảng cách từ I đến mặt phẳng (P) là:
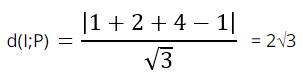
Gọi R là bán kính mặt cầu
⇒ R =√ (r2+d2 ) = 4
Phương trình mặt cầu tâm I, bán kính R = 4 là:
(x-1)2 + (y-2)2 + (z-4)2 = 16
4. Dạng 4: Viết phương trình mặt cầu biết tâm và tiếp xúc với đường thẳng
Phương pháp giải:
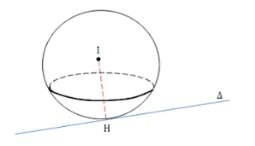
Cho điểm I (a; b; c) và đường thẳng d.
Gọi H là tiếp điểm của đường thẳng d và mặt cầu tâm I. Tìm H.
Khi đó bán kính của mặt cầu R = IH.
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz cho đường thẳng ![]() và điểm I (1; -2; 3). Viết phương trình mặt cầu có tâm I và tiếp xúc với d
và điểm I (1; -2; 3). Viết phương trình mặt cầu có tâm I và tiếp xúc với d
Lời giải
Gọi H là tiếp điểm của đường tròn lớn tâm I và đường thẳng d.
Vì H thuộc d nên H (-1 + 2t; 2 + t; -3 – t). Suy ra IH→ = (2t – 2; t + 4; -t – 6)
Vectơ chỉ phương của d là ud→ = (2, 1, -1)
Vì IH vuông góc với đường thẳng d nên
IH→.ud→ = 0 ⇔ (2t – 2).2 + (t + 4).1 + (-t – 6)(-1) = 0 ⇔ t = 1
Suy ra IH = (-4, 3, -5)
Vì mặt cầu tiếp xúc với đường thẳng nên bán kính của mặt cầu:
R = IH = √(-4)2 + 32 + (-5)2 = 5√2
Vậy phương trình mặt cầu là (x – 1)2 + (y + 2)2 + (z – 3)2 = 50
Ví dụ 2: Cho điểm I (0; 1; 2); B (-1; 1; 0) và C (2; -3; 1). Viết phương trình mặt cầu có tâm I và tiếp xúc với đường thẳng BC
Lời giải:
Đường thẳng BC có VTCP BC→ =( 3;-4; 1)
IB→ = (-1;0; -4)
[IB→ ; BC→ ]=(16;11; -4)
Khoảng cách từ I đến đường thẳng BC là:
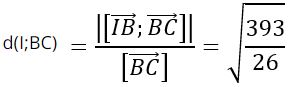
Do mặt cầu tiếp xúc với đường thẳng BC nên khoảng cách từ I đến đường thẳng BC là bán kính mặt cầu tâm I
Vậy phương trình mặt cầu cần tìm là:
x2 + (y-1)2 + (z-2)2 = 393⁄26
5. Dạng 5: Viết phương trình mặt cầu (S) biết tâm I và đường thẳng d cắt mặt cầu theo dây cung AB
Phương pháp:
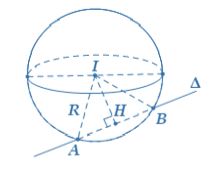
- Bước 1: Tính khoảng cách từ tâm I đến đường thẳng d
- Bước 2: Dựa vào giả thuyết đề cho, ta tính độ dài dây cung AB. Suy ra độ dài AH (với H là trung điểm AB)
Bước 3: Tính IA theo định lý Pytago cho tam giác vuông AIH. Suy ra bán kính R = IA. - Bước 4: Viết phương trình mặt cầu (S) tâm I và bán kính R đã tính bên trên.
Ví dụ 1: Viết phương trình mặt cầu (S) có tâm I (2; 3; -1) và cắt đường thẳng 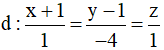 tại hai điểm A, B với AB = 16.
tại hai điểm A, B với AB = 16.
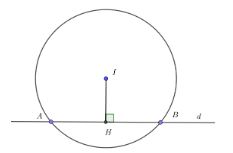
Lời giải
Gọi H là hình chiếu vuông góc của I trên đường thẳng d.
Vì H thuộc d nên H (-1 + t; 1 – 4t; t).
Suy ra IH→ = (t – 3; -4t – 2; t + 1)
Đường thẳng d có vectơ chỉ phương là ud→ = (1, – 4, 1)
Vì IH vuông góc với đường thẳng d nên
IH→.ud→ = 0 ⇔(t-3).1 + (-4t – 2 ).(-4) + (t+1).1 = 0 ⇔ t = -1⁄3
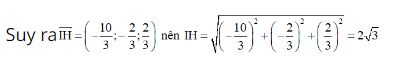
Vì AB = 16 nên HA = 1/2AB = 8
Áp dụng định lí Py – ta – go trong tam giác vuông IAB ta có:
IA2 = TH2 + HA2 = (2√3)2 + 82 = 76 ⇒ IA = 2√19
Vậy bán kính mặt cầu là R = IA = 2√19
Khi đó phương trình mặt cầu là (x – 2)2 + (y – 3)2 + (z + 1)2 = 76
Ví dụ 2: Cho điểm I (0; 0; 3) và đường thẳng 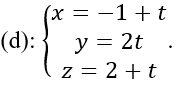 .Viết phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông
.Viết phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông
Lời giải:
Điểm M (-1; 0; 2) ∈ d
⇒ IM→ = (-1;0; -1)
Đường thẳng Δ có một vecto chỉ phương là u→ = (1; 2;1)

⇒ R2 = 8⁄3
Phương trình mặt cầu cần tìm là:
x2 + y2 + (z-3)2 = 8⁄3
6.
6. Dạng 6: Viết phương trình mặt cầu (S) biết tâm I và mặt cầu cắt mặt phẳng (P) theo giao tuyến là đường tròn (C)
Phương pháp giải:
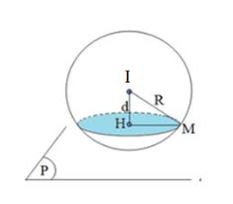
- Bước 1: Tính khoảng cách từ tâm I đến mặt phẳng (P)
- Bước 2: Dựa vào giả thuyết đề cho, ta tính bán kính r của đường tròn giao tuyến. Suy ra bán kính mặt cầu R = √d2(i,(P)) + r2
- Bước 3: Kết luận phương trình mặt cầu (S)
Ví dụ: Cho mặt cầu (S) có tâm I (1; 0; 1) và mặt phẳng (Q): 2x – y + z + 7 = 0. Viết phương trình mặt cầu (S) sao cho (Q) cắt (S) theo một hình tròn có diện tích là 20π
Lời giải
Ta có :
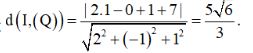
Gọi r là bán kính đường tròn giao tuyến của (S) và mặt phẳng (Q). Ta có diện tích đường tròn giao tuyến là
20π = πr2 ⇒ r = 2√5
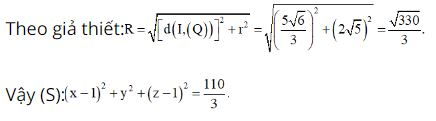
Ví dụ 2: Trong không gian Oxyz, cho mặt phẳng (P): 2x – 3y – z – 2 = 0. Viết phương trình mặt cầu (S) có tâm E thuộc tia Ox sao cho mặt phẳng (P) cách E một khoảng bằng √14 và cắt mặt cầu (S) theo thiết diện là đường tròn có đường kính bằng 4.
Lời giải
Tâm E thuộc tia Ox nên E (a; 0; 0)
Khoảng cách từ E đến mặt phẳng (P) là:

Gọi R là bán kính mặt cầu
Ta có: R = √r2 + h2 = √22 + 14 = √18
Vậy có 2 phương trình mặt cầu thỏa mãn:
(x-8)2 + y2 + z2 = 18
(x+6)2 + y2 + z2 = 18
7. Dạng 7: Phương trình mặt cầu biết tâm thuộc một đường thẳng và thỏa mãn một điều kiện cho trước
Phương pháp giải:
Bước 1: Rút tọa độ tâm I theo đường thẳng d đã cho trước.
Giả sử điểm I là tâm của mặt cầu và đường thẳng d có phương trình 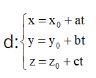
Khi đó nếu I ∈ d thì ta có I(x0 + at; y0 +bt; z0 + ct)
Bước 2: Dựa vào yêu cầu bài toán lập một phương trình theo biến t để giải ⇒Tọa độ tâm I
Bước 3: Xác định bán kính R của mặt cầu
Bước 4: Viết phương trình mặt cầu (S).
Ví dụ 1: Cho hai điểm A(1; -2; 3), B(-1; 0; 1) và mặt phẳng (P): x + y + z + 4 =0. Viết phương trình mặt cầu (S) có bán kính AB/6 có tâm thuộc đường thẳng AB và (S) tiếp xúc với mặt phẳng (P)
Lời giải:
AB→ = (-2;2;-2) ⇒ AB = |AB→ |=2√3
Gọi R là bán kính của mặt cầu (S). Theo giả thiết ta có:
R = AB/6 = √3/3
Đường thẳng AB đi qua A (1; -2; 3) và có một vecto chỉ phương

Với t = 5⁄2 thì I ( -4; 3; -2)
Với t = 7⁄2 thì I ( -6; 5; -4)
Vậy có 2 phương trình mặt cầu thỏa mãn là :
(x+4)2 + (y-3)2 + (z+2)2 = 1⁄3
(x+6)2 + (y-5)2 + (z+4)2 = 1⁄3
Ví dụ 2: Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng 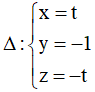 và (S) tiếp xúc với hai mặt phẳng (α): x + 2y + 2z + 3 = 0 và (β): x + 2y + 2z + 7 = 0.
và (S) tiếp xúc với hai mặt phẳng (α): x + 2y + 2z + 3 = 0 và (β): x + 2y + 2z + 7 = 0.
Lời giải
Do I thuộc d nên tâm mặt cầu có tọa độ dạng I (t; -1; -t). Khi đó do (S) tiếp xúc với (P), (Q) nên khoảng cách từ I tới (P), (Q) là bằng nhau và cùng bằng bán kính mặt cầu.
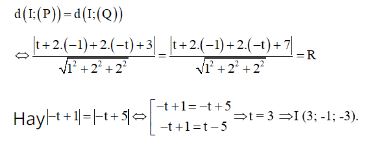
Thay vào phương trình khoảng cách ta được R = 2⁄3. Vậy phương trình mặt cầu:
(x – 3)2 + (y + 1)2 + (z + 3)2 = 4⁄9
Sau khi đọc xong bài viết của chúng tôi có thể giúp các bạn nắm chắc kiến thức về phương trình mặt cầu và các dạng bài tập phương trình mặt cầu thường gặp để vận dụng vào làm bài tập.




